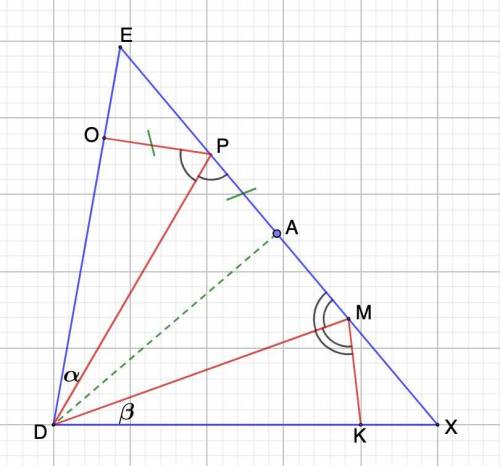
Пошаговое объяснение:
Дано: ΔDEX;
∠EDX = 2∠PDM;
∠OPD = ∠DPX; ∠KMD = ∠DME;
Доказать: OP + KM = PM
Доказательство:
Дополнительное построение.
Отложим отрезок РА = РО.
1. Рассмотрим ΔDOP и ΔDPA.
PA = PO (построение);
∠OPD = ∠DPX (условие)
DP - общая.
⇒ ΔDOP = ΔDPA (по двум сторонам и углу между ними. 1 признак)
В равных треугольниках против равных сторон лежат равные углы.⇒ ∠ODP = ∠PDA
2. Пусть ∠ODP = α, а ∠MDX = β.
∠EDX = 2∠PDM (по условию)
⇒ ∠PDM = α + β
∠ODP = ∠PDA = α (п.1)
⇒ ∠ADM = ∠PDM - ∠PDA = α + β - α = β
3. Рассмотрим ΔDAM и ΔDMK.
∠ADM = ∠MDK = β (п.2)
∠KMD = ∠DME (условие)
DM - общая.
⇒ ΔDAM = ΔDMK (по стороне и двум прилежащим углам. 2 признак)
В равных треугольниках против равных углов лежат равные стороны.⇒ АМ = МК
4. РМ = РА + АМ или РМ = PO + KM.
Пусть х - меньшее число, тогда 5х - большее число. Сумма двух чисел равна 240. Уравнение:
х + 5х = 240
6х = 240
х = 240 : 6
х = 40 - меньшее число
5х = 5 · 40 = 200 - большее число
Вiдповiдь: 40 - менше з цих чисел.