Відповідь:
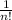
Покрокове роз'яснення:
Простір елементарних подій (Ω), тобто кількість усіх рівноможливих результатів цього стохастичного (випадкового) експерименту, дорівнює перестановкам із чисел 1, 2, 3, ..., n. (n! послідовностей)
Ну і дійсно: нам же потрібно визначити, які можуть бути різні комбінації із чисел при витягуванні їх для того, щоб дізнатися, скільки є рівноможливих наслідків цього експерименту.
Якщо їх (чисел), до прикладу, буде 3, то нам потрібно визначити скільки є комбінацій із цих чисел без повторень, тобто 3! (для формули потрібно, якщо хтось ще не зрозумів)
Відповідно, кількість усіх рівноможливих результатів деякого стохастичного (випадкового) експерименту, при якому ми б послідовно витягували усі числа, пронумерованих як 1, 2, 3, ..., n, дорівнюють кількості перестановок із цих чисел, тобто n!
Сприятлива подія полягає в тому, що при витягуванні послідовно n чисел, послідовність вийде зростаючою. Така подія 1 - вона і є сприятливою.
То тепер, нехай A - це подія, при якій утвориться зростаюча послідовність, а P(A) - її ймовірність. Тоді:
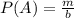 , де b - кількість рівноможливих наслідків цього експерименту (n!), а m - це наслідки події A, тобто сприятливі події (1).
, де b - кількість рівноможливих наслідків цього експерименту (n!), а m - це наслідки події A, тобто сприятливі події (1).
Відповідно маємо:
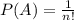
1. х = 3; у = 2
3. х = 6; у = 2
Пошаговое объяснение:
1.
х/3 - у/4 = 1/2
х/2 + 3у/5 = 2,7
Избавимся от дробей домножением левой и правой части двух уравнений:
Первое уравнение домножим на 12 (НОК чисел 3,4,2)
12*х/3 - 12*у/4 = 12*1/2
4х - 3у = 6 - первое уравнение
Второе уравнение домножим на 10 (НОК чисел 2,5,10)
10*х/2 + 10*3у/5 = 10*2,7
5х + 6у = 27 - второе уравнение
Далее решим систему уравнений:
1. 4х - 3у = 6 I *2 (домножим первое уравнение на 2)
5х + 6у = 27
2. 8х - 6у = 12
5х + 6у = 27
Сложим левую и правую части уравнений:
13х = 39
х = 39/3
х = 3 → подставим значение х в первое уравнение: 8х - 6у = 12 и вычислим значение у:
8*3 - 6у = 12
-6у = 12 - 24
-6у = -12
у = -12/(-6) = 2
Проверим: подставим значения х и у в уравнения:
х/3 - у/4 = 1/2 → 3/3 - 2/4 = 1/2 → 1 - 1/2 = 1/2 → 1/2 = 1/2
х/2 + 3у/5 = 2,7 → 3/2 + 6/5 = 2,7 → 1,5 + 1,2 = 2,7 → 2,7 = 2,7
3. Это уравнение решаем точно таким
х/3 - у/2 = 1
х/4 + у/5 = 1,9 = 19/10
Избавимся от дробей домножением левой и правой части двух уравнений:
Первое уравнение домножим на 6 (НОК чисел 3,2)
6*х/3 - 6*у/2 = 1*6
2х - 3у = 6 - первое уравнение
Второе уравнение домножим на 20 (НОК чисел 4,5,10)
20*х/4 + 20*у/5 = 20*19/10
5х + 4у = 38 - второе уравнение
Далее решим систему уравнений:
1. 2х - 3у = 6 I *4 (домножим первое уравнение на 4)
5х + 4у = 38 I *3 (домножим второе уравнение на 3)
2. 8х - 12у = 24
15х + 12у = 114
Сложим левую и правую части уравнений:
23х = 138
х = 138/23
х = 6 → подставим значение х в первое уравнение: 8х - 12у = 24 и вычислим значение у:
8*6 - 12у = 24
-12у = 24 - 48
-12у = -24
у = -24/(-12) = 2
Проверим: подставим значения х и у в уравнения:
х/3 - у/2 = 1 → 6/3 - 2/2 = 1 → 2 - 1 = 1 → 1 = 1
х/4 + у/5 = 1,9 → 6/4 + 2/5 = 1,9 → 1,5 + 0,4 = 1,9 → 1,9 = 1,9