Чертёж ниже, кликни
1)По условию AK : AN = 1 : 3.
Отсюда
АК = 1 часть
AN = 3 части
NК = 1 + 3 = 4 части
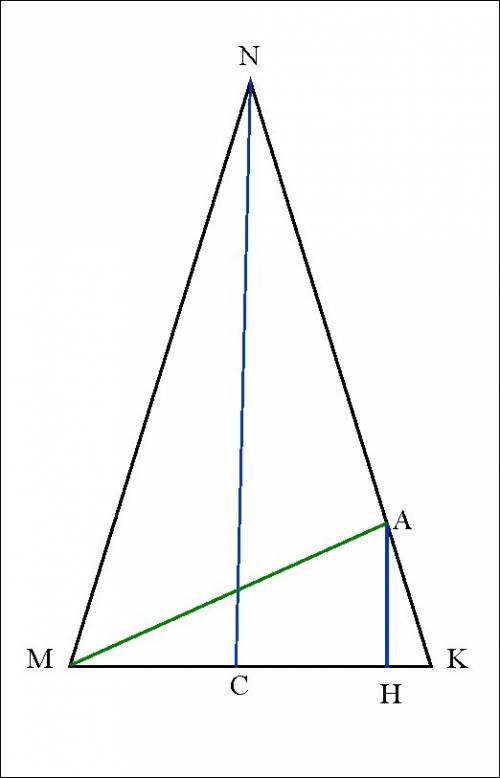
2)Проведем высоту NC,
CК= МК/2 = 5 см.
3)По теореме Пифагора найдем NC из прямогольного Δ NСК.
NC = √(NK² - CK²) = √(20² - 5²) = √ 375 = 5√15.
4)Опустим из точки А перпендикуляр АH на сторону МК.
5)Δ CКN подобен ΔHКА, т. к. АH||NC и оба прямоугольные.
6)Чтобы найти АН составим пропорцию соответственных сторон:
CN: AH = NК : АК
5√15 : АH = 4 : 1
АH= 5√15/4.
7)Чтобы найти НК составим пропорцию соответственных сторон:
CК: HК = NК: АК
5 : HК = 4 : 1
HК = 5/4 = 1,25.
8)Теперь найдем МH:
МН = MK - HK = 10 - 1,25 = 8,75.
9)Из прямоугольного Δ МАН по теореме Пифагора найдём, наконец, АМ:
АМ= √(МН² + АН²) = √(8,75)² + (5√15/4)² =
√(76,5625 + 375/16) = √(76,5625 + 23,4375) = √100 = 10 см
ответ: 10 см.
Рассуждения таковы- число 2017 - равно сумме чисел, у которых последняя только цифра разная. Все остальные - одинаковые.
Поделим 2017 на 9 нацело.
Получится 224.
Значит, числа будут вида 22х (таких чисел будет 9), либо 220+х, где х - разные цифры
Дальше
2017-220*9=37
Т.е 9 разных чисел от 0 до 9( т.е. одну из этого ряда нужно убрать) должны давать в сумме 37.
Сумма чисел от 0 до 9 будет=45
45-37=8 Вот как раз эту цифру и нужно убрать.
Остальные от 0 до 9 приписать к 22х
2017=220+221+...+227+229