На олимпиаде было 9 задач. Каждый участник решил ровно три задачи, каждые двое решили разные наборы задач, а для любых троих нашлась хотя бы одна задача, не решённая никем из них. Могло ли число участников этой олимпиады быть больше 55? Кто ответит не правильно то подам жалобу
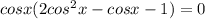
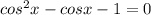
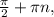, n∈Z или cosx=1, x=2πm, m∈Z или cosx= - 1/2. x=
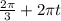, t∈Z или x= - 
, k∈z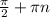
≤ - π поделим все части неравенства на π, получим,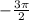 
, 
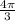
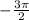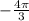
Обозначим катеты треугольника АВС как: АС=b, ВС=а, а гипотенуза равна по условию АВ=АД+ДВ=13.
Составим систему уравнений, опираясь на теорему Пифагора:
b^2+a^2=169
b^2-81=a^2-16 (Это равенство получается из того, что левая и правые части равны CД^2)
b^2=117
Найдем СД.
СД^2=b^2-81=117-81=36 => СД=6