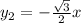Зачем? лучше, чем крылов, вряд ли кто-то придумает, если даже готовую мораль без ошибок не могут списать. однажды деткам где-то в школе по программе решили творчество крылова преподать и каждый отрок, поскрипев мозгами, был должен басню "под крылова" наклепать. ворону с сыром принесли, свинью под дубом- чтоб атмосферу творчества создать, да с моськой, говорят, была проблема - её никто так и не смог поймать.. к концу урока сочиненья сдали и, чтобы авторам хвалу и честь воздать найлучшие творенья зачитали, но лавры оказалось некому вручать ведь хоть с оригиналом стих был сходен- был посрамлен лирический творец берись за то, к чему ты сроден коль хочешь, чтоб в делах успешен был конец".
Пусть уравнение асимптоты к гиперболе: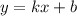 , где
, где 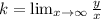 , а
, а 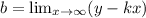
Найдём значения k и b для 2 случаев:
Случай первый:
Итого, первая асимптота: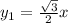
Случай второй:
Вторая асимптота: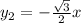
ответ: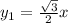 ,
,