В правильной пирамиде медиана боковой грани к основанию - это апофема А.
Сторона основания а и основание боковой грани а равны по 1.
Находим апофему: A = 2S/a = 2*1/1 = 2.
По свойству медиан точка М делит апофему в отношении 2:1 от вершины. SM = (2/3)*2 = 4/3, МК = (1/3)*2 = 2/3.
Находим высоту пирамиды: H = √(2² - (1/2)²) = √15/2.
Находим косинус и синус угла α между основанием пирамиды и боковой гранью.
cos α = (1/2)/2 = 1/4, sin α = (√15/2)/2 = √15/4.
Косинус угла при вершине пирамиды (назовём его S) равен:
cos S = (22 + 22 – 12)/(2*2*2) = 7/8, синус равен √(1 – (49/64)) = √15/8.
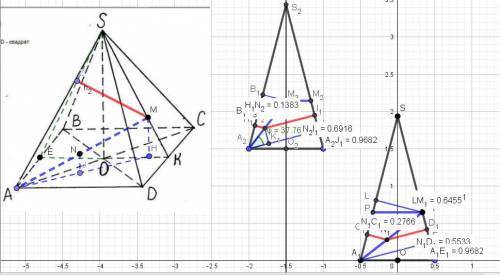
Проведём два осевых сечения пирамиды перпендикулярно смежным сторонам основания и спроецируем на эти плоскости точки M и N (они даны на прилагаемых рисунках).
Расстояния от точек М и N до граней пирамиды обозначим буквой h.
До основания: h(М) = (1/3) H = (1/3)*(√15/2) = √15/6.
h(N) = (3/7) hM = (3/7)*(√15/6) = √15/14.
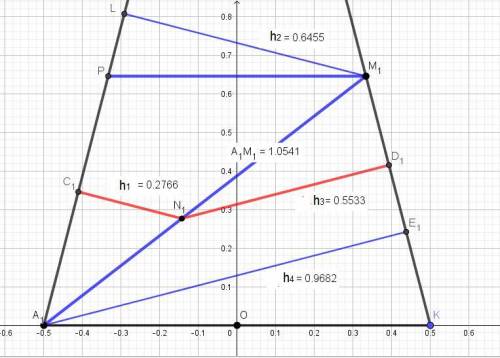
До грани, содержащую точку М, и противоположную ей.
Высота h2 = SM*sin S = (4/3)*(√15/8) = √15/6.
h1 = (3/7) h2 = (3/7)*(√15/6) = √15/14.
Высота h4 = a*sin α = 1*(√15/4) = √15/4.
h3 = (4/7) h4 = (4/7)*(√15/4) = √15/7.
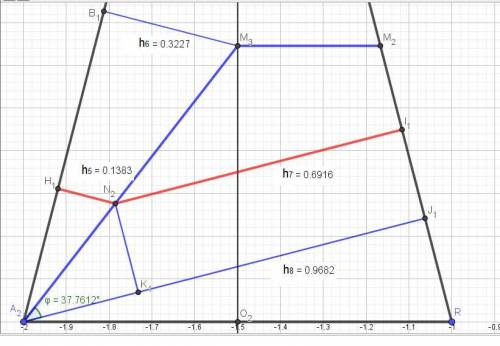
Рассмотрим второе сечение.
Высота h6 = SM3*sin (S/2) = (2/3)*H*((1/2)/2) = (2/3)*(√15/2)*(1/4) = √15/12.
h5 = (3/7) h6 = (3/7)*(√15/12) = √15/28.
Высота h8 = a*sin α = 1*(√15/4) = √15/4.
Для определения высоты h7 найдём угол φ.
φ = arc tg(M3O/(a/2)) – (90º - arc sin α) = arc tg((√15/6)/(1/2)) – arc sin(√15/4) = arc tg((√15/3) – arc sin(√15/4) = 52,23875609º – (90º - 75,52248781º) =
= 37,76124391º.
cos φ = 0,790569.
Найдём длину проекции отрезка АМ на секущую плоскость SEK по теореме косинусов: AM = √(12 + (2/3)² - 2*1*(2/3)*(1/4)) = √(1 + (4/9) – (1/3)) = √10/3.
Тогда AN = (3/7)AM = (3/7)*( √10/3) = √10/7.
Отсюда h7 = h8 – AN*cos φ = √15/4 – (√15/7)*0,790569 = 0,691604.
Сложим длины всех заданных высот:
Σh = (√15/14) + (√15/14) + (√15/7) + (√15/28) + 0,691604 = 1,936492.
Все плохо, разложить на "красивые" множители нельзя
3. Решаем формулой Кардано4. Сделаем заменутогда уравнение имеет вид

5. Определим величину Q
6. Тогда определим величины а и b![y_2=\dfrac13\sqrt[6]{79507}\cos\Bigg(\dfrac13\b{arctg}\bigg(\dfrac{3\sqrt{4119}}{206}\bigg)\Bigg)-\sqrt3\cdot\dfrac13\sqrt[6]{79507}\sin\Bigg(\dfrac13\b{arctg}\bigg(\dfrac{3\sqrt{4119}}{206}\bigg)\Bigg)](/tpl/images/1463/8874/75333.png)
![y_3=\dfrac13\sqrt[6]{79507}\cos\Bigg(\dfrac13\b{arctg}\bigg(\dfrac{3\sqrt{4119}}{206}\bigg)\Bigg)+\sqrt3\cdot\dfrac13\sqrt[6]{79507}\sin\Bigg(\dfrac13\b{arctg}\bigg(\dfrac{3\sqrt{4119}}{206}\bigg)\Bigg)](/tpl/images/1463/8874/a3944.png)
Мы нашли у - теперь найдем х