
Классическая вероятность события:
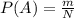 ,
,
где P(A) — вероятность события A;
m — число благоприятных событий;
N — число всех возможных событий.
1) событие A — книга будет на эстонском, m — 6, N — 6+4=10
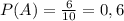
2) событие A₁ — книга с 1-й полки будет на эстонском, m — 6, N — 6+4=10
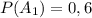
событие B₁ — книга со 2-й полки будет на эстонском, m — 5, N — 5+3=8
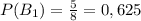
Произведение совместных событий:
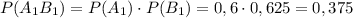
событие A₂ — книга с 1-й полки будет на английском:
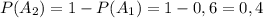
событие B₂ — книга со 2-й полки будет на английском:
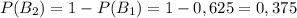
Произведение совместных событий:
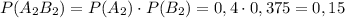
Сумма совместных событий:
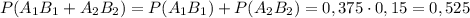
1) 0,6 или 60% ;
2) 0,525 или 52,5%
∠А=65°
Если четырёхугольник вписан в окружность, то суммы величин его противоположных углов равны 180°.
Отсюда следует, что вписать в окружность можно только равнобокую трапецию.
Трапеция ABCD- равнобедренная.
Рассмотрим параллельные прямые ВС , АD и секущую АС,
∠АСВ=∠CAD - как накрест лежащие углы,
∠СВD=∠АСВ -как равные углы при основе равнобедренного треугольника ВОС( точка О- точка пересечения диагоналей трапеции)
∠В=80°+35°=115°
Свойства трапеции
Сумма углов, прилежащих к боковой стороне трапеции, равна 180∘
∠А+∠В=180° → ∠А=180°-∠В=180°-115°=65°
Вариант 2
∠CAD- вписанный, он опирается на дугу ∪ СD
так как СD=AB, то ∠АСВ=∠CAD=35°,
ΔАОС- равнобедренный, ∠АСВ=∠СВD=35°,∠ВОС=180°-2*35°=110°( по теореме о сумме трёх углов треугольника)
∠АОВ=180°-∠ВОС=180°-110°=70°( как смежные углы)
в ΔАОВ ∠ВАО=180°-80°-70°=30°
∠А=∠ВАО+∠CAD=30°+35°=65°
Пошаговое объяснение:
11 в квадрате это 121. переносим 6/8 за равно что бы было х = ( (179-121)/32 ) * 8/6(переворачиваем 6/8 так как мы перенесли за равно) и вычисляем получилось 29/12 это ответ Е 2(5/12)