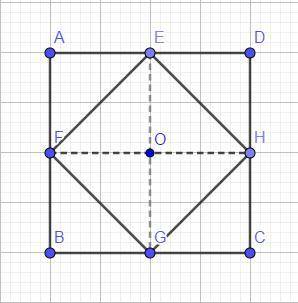
Квадрат ABCD; E - середина AD, F - середина AB, G - середина BC, H - середина CD (рисунок в приложении).
Найти:Площадь четырехугольника EFGH.
Решение:Вариант 1.
Проведем диагонали EG и FH четырехугольника EFGH (пусть они пересекаются в точке O). Так как они соединяют середины противоположных сторон квадрата, они делят его на 4 других равных квадрата: AFOE, BFOG, CHOG и DHOE. В каждом из них проведена диагональ. А диагональ делит сам квадрат на две равные по площади части (и не только по площади). Так как площадь четырехугольника EFGH (на самом деле это тоже квадрат) занимает половину площади каждого из квадратов AFOE, BFOG, CHOG и DHOE, то она равна половине ABCD, то есть:
S(EFGH) = 4 · 4 : 2 = 8 (см²)
Вариант 2.
Можно воспользоваться тем, что площадь параллелограмма Вариньона (параллелограмма, соединяющего середины сторон произвольного четырехугольника) всегда равна половине площади исходного четырехугольника. Значит:
S (EFGH) = S (ABCD) / 2 = 4² / 2 = 16 / 2 = 8 (см²)
ответ: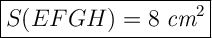
Пусть х - первый катет, х-2 - второй.
Сначала найдём катеты за теоремой Пифагора:
гипотенуза в кв. = 1 катет в кв.+2 катет в кв.
с в кв. = а в кв.+в в кв.
10 в кв. = х в кв.+(х-2) в кв.
100 = х в кв.+ х в кв.-4х+4
2х в кв.-4х-96 = 0 /2
разделим на 2:
х в кв.-2х - 48 = 0
D = b^2-4*ac
^2 - это значит в квадрате
D = 2*2-4*1*(-48)= 4+192 = 196
корень из 196 = 14
х = -b+- корень D/2а
х = (2+14)/2 = 16/2=8
х = 8 -первый катет.
8-2 = 6 - второй катет.
Проверяем:
6*6 + 8*8 = 36+64 = 100 = 10*10
площадь пр. треуг. = а*в/2
8*6/2 = 24 - площадь.
ответ: 24 площадь треугольника.