Поставьте знаки « + », «-», « × », «:» и скобки так, чтобы в итоге получилось 1 (при необходимости минус можно ставить и перед первой цифрой) 1 2 3 4 5 6 7.

👇

Увидеть ответ

Ответ:

NastenkaDrow

20.05.2023

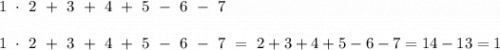
$1~\cdot~2~+~3~+~4~+~5~-~6~-~7 \\\\1~\cdot~2~+~3~+~4~+~5~-~6~-~7~=~2+3+4+5-6-7=14-13=1$

4,5(53 оценок)

Открыть все ответы

Ответ:

Lovedashuta

20.05.2023

ответ: 26; 15; 64;250;24

Пошаговое объяснение:

Делаем задания через определенные интегралы и первообразные:

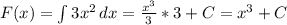
$F(x) = \int{3x^2} \, dx = \frac{x^3}{3} *3+C = x^3 +C$

Подставляем в первообразную границы интегрирования:

$\int\limits^3_1 {3x^2} \, dx = F(3) - F(1) = 26$

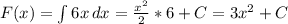
$F(x) = \int{6x} \, dx = \frac{x^2}{2} *6+C = 3x^2 +C$

Подставляем в первообразную границы интегрирования:

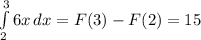
$\int\limits^3_2 {6x} \, dx = F(3) - F(2) = 15$

$F(x) = \int{8x} \, dx = \frac{x^2}{2} *8+C = 4x^2 +C$

Подставляем в первообразную границы интегрирования:

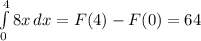
$\int\limits^4_0 {8x} \, dx = F(4) - F(0) = 64$

Производим ровно те же операции, что и до этого, так как требуется найти путь у параболы ветвями вверх => интеграл не будет отрицательным.

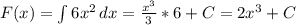
$F(x) = \int{6x^2} \, dx = \frac{x^3}{3} *6+C = 2x^3 +C$

Подставляем в первообразную границы интегрирования:

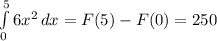
$\int\limits^5_0 {6x^2} \, dx = F(5) - F(0) = 250$

Находим первообразную заданной функции:

$F(x) = \int{2x+5} \, dx = \int{2x} \, dx + \int{5} \, dx= \frac{x^2}{2} *2 + 5x +C = x^2 + 5x+C$

Ограничивающие прямые - те же границы интегрирования:

$\int\limits^3_0 {2x+5} \, dx = F(3) - F(0) = 24$

4,6(41 оценок)

Ответ:

gybshova

20.05.2023

Пусть имеется n различных объектов.

Будем переставлять их всеми возможными число объектов остается неизменными, меняется только их порядок). Получившиеся комбинации называются перестановками, а их число равно

перестановки, формулы комбинаторики

Pn=n!=1⋅2⋅3⋅...⋅(n−1)⋅n

Символ n! называется факториалом и обозначает произведение всех целых чисел от 1 до n. По определению, считают, что 0!=1,1!=1.

Пример всех перестановок из n=3 объектов (различных фигур) - на картинке справа. Согласно формуле, их должно быть ровно P3=3!=1⋅2⋅3=6, так и получается.

С ростом числа объектов количество перестановок очень быстро растет и изображать их наглядно становится затруднительно. Например, число перестановок из 10 предметов - уже 3628800 (больше 3 миллионов!).

4,4(90 оценок)

Это интересно:

Кулинария-и-гостеприимство

07.03.2023

Как приготовить пончики: простой и вкусный рецепт...

28.09.2020

Как медитировать, если вы подросток...

02.12.2021

Как распознавать СДВГ у взрослых: симптомы и диагностика...

Хобби-и-рукоделие

19.02.2020

Как начать бизнес по производству самодельного мыла...