Большая сторона первоначального прямоугольника x.
Есть два возможный варианта: 1) прямоугольник разрезали по меньшей стороне; 2) прямоугольник разрезали по большей стороне. Рассмотрим их оба:
1) пусть одна сторона первого прямоугольника y, тогда вторая 6-y. Вторые стороны у обоих x.
Площади: xy кв.ед. у первого, x·(6-y) кв.ед. у второго. У первого в 3 раза больше:
xy = 3x·(6-y)
Периметры: (x+y)·2 у первого, (x+6-y)·2 у второго. У первого в 2 раза больше:
(x+y)·2 = 2·(x+6-y)·2
Составим и решим систему уравнений:

Большая сторона первоначального прямоугольника 1,5.
2) пусть одна сторона первого прямоугольника y, тогда вторая x-y. Вторые стороны у обоих 6.
Площади: 6y кв.ед. у первого, 6(x-y) кв.ед. у второго. У первого в 3 раза больше:
6y = 3·6(x-y)
Периметры: у первого (y+6)·2, у второго (x-y+6)·2, у первого в 2 раза больше:
(y+6)·2 = 2·(x-y+6)·2.
Составим и решим систему уравнений:
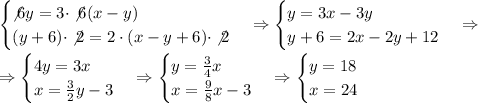
Большая сторона первоначального прямоугольника 24.
ответ: 1,5 или 24.
Первая труба - 24 минут.
Вторая труба - 40 минут.
Найти - обе трубы ?
1) (возьмем наполнение всего бассейна за одну целую) 1 : 24 = 1/24 часть - бассейна может заполнить первая труба за одну минуту, так как она может заполнить весь бассейн за 24 минуты;
2) 1 : 40 = 1/40 часть - бассейна может заполнить вторая труба за одну минуту, так как она может заполнить весь бассейн за 40 минут;
3) 1/24 + 1/40 = 5/120 + 3/120 = 8/120 = 1/15 части - бассейна могут заполнить две трубы за одну минуту, работая вместе;
4) 1 : 1/15 = 1 * 15/1 = 15 минут - смогут наполнять бассейн обе эти трубы.
ответ: за 15 минут.
а) 1+4/9+2+5/18=3+/13/18.
б) 3+5/12-1+7/24=2+3/24.
в) 3+1/5×3+1/8=10.
г) 1+4/11:1+2/13=13/11=1+2/11.