а) Если чисел выписано 7, то их было задумано 3. Их не могло быть меньше (у двух чисел сумм выписывается всего 3), и не могло быть больше (у четырёх чисел сумм будет 15). Нуля в наборе нет, а есть положительные и отрицательные числа. Какое-то встречается один раз, а какое-то два. Если отрицательное число одно, то положительных два, но тогда из них формируются три положительные суммы. Значит, было два отрицательных числа и одно положительное число, равное 7. Из отрицательных чисел может быть сформировано -5, чтобы в сумме с 7 получалось 2. Сумма же отрицательных чисел равна -13. Значит, это числа -8 и -5. А весь набор задуманных чисел был такой: -8, -5, 7. Легко видеть, что этот вариант подходит.
б) Пример с пятью числами: -2,-1,0,1,2. Легко проверяется, что выписано будет 31 число, где ±3 появляется 2 раза, ±2 -- 4 раза, ±1 -- 6 раз, и 0 появится ровно 7 раз. Четырёх различных чисел недостаточно. Это легко проверяется, так как 0 сам по себе встречается не более одного раза, среди пар он встречается не более двух раз (пары с одинаковой суммой не пересекаются), среди троек не более одного раза (все их суммы различны), и как сумма всех чисел тоже не более одного раза -- итого получается меньше семи.
в) Нет, не всегда. Пусть задуманы числа 1, 2, -3. Из них формируется набор чисел от -3 до 3 (без повторений). Ясно, что если у всех задуманных чисел сменить знак, то получится то же самое, поэтому задуманы могли быть и числа -1, -2, 3.
Собственно, вот в этой задаче я уже решал, но почему-то пропали прикреплённые картинки. По этой причине повторюсь.
Если принять сторону основания за a, a ребро за b, то в зависимости от расчёта приходим к одной из формул (они приводимы друг к другу):
Сначала доказываете, что плоскость BMD перпендикулярна AC, далее - перпендикулярна A'C', A'C' пересекает BMD в точке P, ну и перпендикулярна всем прямым данной плоскости, проходящим через P => ND перпендикулярна A'C'.
Т.о.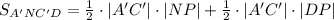
т.е.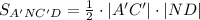
Найдём длины нужных нам в дальнейшем отрезков:
В треугольнике BMD DM и MO это медианы, пересекающиеся в точке P. Т.о.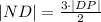
AC || A'C' из подобия треугольников AMC и A'MC' следует, что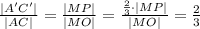
т.е.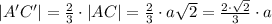
Теперь подставляем значения в формулу:
ответ: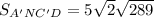
P.S.> Для примера - есть вариант, где a=6, b=12. В этом случае результат будет следующий:
Это соответствует правильному ответу.
P.P.S.> Попробую прикрепить ещё снимки решения на бумаге (если получится) - там 2 варианта. Почему-то не всегда прикреплённые картинки сохраняются. По этому и вбил решение текстом.