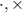. Второй используется в случае переноса на новую строку или для наглядности. Например,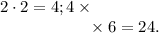 
, но в начальной школе про это можно не знать. Числа, соединённые знаком умножения, называют множителями, а результат операции - произведением.
, либо записывают в виде дроби: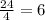 
.
1)9/30 20/30
2)36/45 20/45
3)7/14 2/14
4)55/88 56/88
(вроде так)
Пошаговое объяснение:
1)3/10 2/3=9/30 20/30
Нок(10,3)=30(тк 3 прсотое число)
2)4/5 4/9=36/45 20/45
Нок(5,9)=45(тк 5 простое чило)
3)1/2 1/7=7/14 2/14
Нок(2,7)= 14(тк 7 простое число)
4)5/8 7/11=55/88 56/88
Нок(8,11)=88(тк 11 простое число)