3 6 9 12 15 18 21 24 27 30 33 36 39 42 45 48 51 54 57 60 63 66 69 72 75 78 81 84 87 90 93 96
99 102 105 108 111 114 117 120 123 126 129 132 135 138 141 144 147=3675
1.Приведите примеры обыкновенных дробей. 1/3 29/80
2.Числитель дроби – это… число над дробной чертой
3.Знаменатель дроби – это… число под дробной чертой
4.Рациональное число – это число, которое… может быть представлено в виде дроби
5.Натуральное число можно записать в виде дроби… со знаменателем 1.
6.Приведите пример для пункта 5. 10/1 43/1
7.Как можно получить дробь, равную данной дроби? … Умножить числитель и знаменатель на одно и то же число.
8.Приведите пример к пункту 7. 1/5 = 2/10; 3/4 = 9/12
9.Как можно сократить дробь? … Разделить числитель и знаменатель на одно и то же число.
10.Приведите пример к пункту 9. 5/20 = 1/4
11.Какую дробь называют несократимой? Если числитель и знаменатель нельзя разделить на одно и то же число
12. Приведите пример к пункту 11. 33/58
13.Чему равна дробь, числитель и знаменатель которой равны? единице
14.Приведите пример к пункту 13. 11/11 = 1
15.Сформулируйте алгоритм приведения двух дробей к наименьшему общему знаменателю. Для приведения дробей к общему знаменателю надо: разделить наименьший общий знаменатель на знаменатели данных дробей, т. е. найти для каждой дроби дополнительный множитель; умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.
16.Уметь решать задания типа №798-803
17.Пять правил сравнения дробей. Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше. Из двух дробей с одинаковыми числителями больше та дробь, у которой знаменатель меньше. Чтобы сравнить две дроби с разными числителями и знаменателями, надо найти их общий знаменатель.
18. Уметь решать задания типа №809-815
19.Два правила сложения дробей. Чтобы сложить две обыкновенные дроби, следует: привести дроби к наименьшему общему знаменателю; сложить числители дробей, а знаменатель оставить без изменений; сократить полученную дробь; если получилась неправильная дробь преобразовать неправильную дробь в смешанную.
20.Какая дробь называется правильной? у которой числитель меньше знаменателя 3/8
21.Какая дробь называется неправильной? у которой числитель больше знаменателя 11/5
22.Два закона сложения. Переместительный закон сложения: от перемены мест слагаемых сумма не меняется. Сочетательный закон сложения: чтобы к сумме двух чисел прибавить третье число, можно к первому числу прибавить сумму второго и третьего чисел.
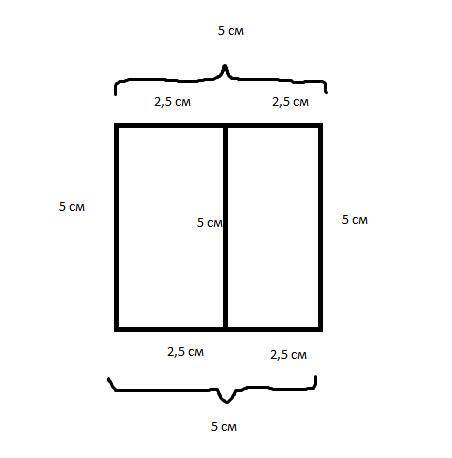
Квадрат, периметр которого 20 см, разрезали на два одинаковых прямоугольника. На сколько сантиметров периметр квадрата меньше суммы периметров полученных прямоугольников? Сделай рисунок и реши задачу.
Если периметр квадрата 20 см, то каждая из его сторон равна 20/4 = 5 см. Значит две противоположные стороны каждого из двух прямоугольников также равны 5 см, а две остальные равны половине стороны квадрата, то есть 5/2 = 2,5 см. Рассчитаем периметр одного из прямоугольников: P(прямоугольника) = 2 · (a + b) = 2 · 2,5 + 2 · 5 = 5 + 10 = 15 (см). Так как прямоугольников два, то сумма их периметров будет равна 2 · 15 = 30 см. Чтобы узнать на сколько сантиметров периметр квадрата меньше суммы периметров полученных прямоугольников, нужно из суммы периметров прямоугольников отнять периметр квадрата: 30 - 20 = 10 см.
ответ: на 10 см периметр квадрата меньше суммы периметров полученных прямоугольников.
Всё решается очень просто.
Если числа кратны трём, то первое число будет 3, последнее будет 150.
Надо использовать свойство арифметической прогрессии.
S=n*(a(1)+a(n))/2
a(1)=3
a(n)=150
Осталось только лишь посчитать количество чисел между 3 и 150 кратные 3:
150=3+(n-1)*3
n=50 чисел
Осталось только известные числа подставить в первую формулу, и получится ответ.
Вот и всё решение.