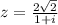
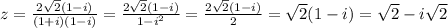
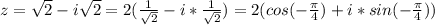
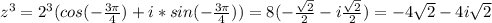
Пусть это число abcd Если оно делится на 36, то оно делится на 4 и на 9.Сумма его цифр 18, значит оно точно делится на 9. Чтобы число делилось на 4, нужно, чтобы две его последние цифры образовали число делящееся на 4.
т.к. 2000<abcd < 2400, то а=2, b может принимать значения 1, 2 или 3 .
Сумма b+c+d=18-2=16 и d- четное. Рассмотрим случаи
d=0, значит b+c=16, зная что b≤3, а 1≥с≥9, то подходящих вариантов нетd=2, значит b+c=16-2=14, зная что b≤3, а 1≥с≥9, то подходящих вариантов нетd=4, значит b+c=16-4=12, то подходит b=3 c=9,но 94:4.d=6, значит b+c=16-6=10. 1+9 (96 делится на 4), получаем 21962+8 (86 не делится на 4)3+7 (76 делится на 4), получаем 2376d=8, значит b+c=16-8=81+7 (78 не делится на 4)2+6 (68 делится на 4), получаем 22683+5 (58 не делится на 4)ответ: 2196 или 2268 или 2376
6^cos4x*6^cos6x=6^cos5x
вынесем 6
6(cos4x*cos6x) = 6^cos5x
шестерки сокращаются
остается
cos4x*cos6x = cos5x
раскладываем по формуле:
cos (а)*cos (b) = 1/2 ( cos (a-b) + cos (a+b))
1/2 (cos2x + cos10x) = cos5x
1/2 cos12x - cos 5x = 0 (делим оль на 1/2, остется 0)
cos 7x = 0
Частный случай тригонометрического уравнения.
7x = п/2 + пк
где п - число пи, а к - число оборотов (повторов)
х = п/14 + 7 пк.