Пошаговое объяснение:
а) разделил на 2 интеграла по разности, под первым e^(pi) - константа, поэтому получится e^(pi) * x = pi* e^(pi) - 0 ( при подстановке)
второй - табличный = sinx + C = 0 в подстановке.
ответ: pi* e^(pi)
б) занесу cosx под дифференциал
cosxdx = d ( sinx + 1)
дальше простой степенной интеграл = 1/3*(1+sinx)^3 + C = 1/3 * (1)^3 - 1/3 * (1)^3 = 0
в) опять под дифференциал
d(4-t^2) = -2*t dt => tdt = -1/2 * d(4-t^2)
дальше простой степенной интеграл = -1/2*2*(4-t)^(1/2) + C = -3^(1/2) + 4^(1/2) = 2 - 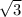
г) под дифференциал:
d(1 + 4x^3) = 12x^2 dx => 6x^2dx = 1/2 d(1+4x^3)
дальше табличный интеграл = 1/2 * ln(1+4x^3) + C = 1/2*ln5 - 1/2*ln1 = 1/2*ln5
1)14,3 • 0,6 -5,7 • 1,4
14,3*0,6 = 8,58
5.7*1.4=7.98
8.58-7.98= 0.6
2)(54-23,42) • 0,08
54-23,42= 30,58
30,58*0,08 = 2,4464
3)(4,125 – 1,6) • (0,12 +7,3)
4,125 – 1,6 = 2,525
0,12 +7,3 = 7,42
7,42 × 2,525 = 18,7355
4)(139-23,48) : 38 + 4,35 • 18
139-23,48 = 115,52
115,52 : 38 = 3,04
4,35 * 18 = 78,3
78,3 + 3,04 = 81,34
5)(1,87+1,955) : 0,85 –(3 • 1,75 – 2,5) • 1,62
1,87 + 1,955 = 3,825
3 * 1,75 = 5,25, 5,05 - 2,5 = 2,75
3,825 / 0,85 - 2,75 * 1,62
4,5 - 4,455 = 0,045.
6)1,24 : 3,1+12 : 0,25 - 2 : 25 + 18 : 0,45
1, 24 : 3,1 = 0,4;
12 : 0, 25 = 48;
2 : 25 = 0,08;
18 : 0,45 = 40;
0,4 + 48 = 48,4;
48,4 - 0,08 = 48,32;
48,32 + 40 = 88,32.
7)52-(15,54 : 1,48 + 3,4) • 2,8
15,54:1,48=10,5
10,5+3,4=13,9
13,9*2,8=38,92
52-38,92=13,08