При каждом броске симметричной монеты возможны два исхода - {выпал орел} и {выпала решка}. Так как монета была подброшена 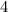 раза, то всего исходов может быть
раза, то всего исходов может быть 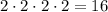 (количество исходов при каждом броске независимо, поэтому двойки перемножаются).
(количество исходов при каждом броске независимо, поэтому двойки перемножаются).
Нам подходят всего лишь четыре исхода (О - орел, Р - решка): ОООР, ООРО, ОРОО и РООО (если без перебора в четыре случая, то 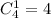 исхода).
исхода).
Так как при равновозможных элементарных исходах вероятность - это отношение числа благоприятных исходов ко всем исходом, то:
P = {число исходов, в которых выпало ровно три орла} / {число всех возможных исходов} = 4 / 16 = 1 / 4 = 0,25.
Задача решена!
ответ: 0,25 .
5. При решении задачи применяется принцип Дирихле : в любой совокупности из n множеств, соде в общей сложности более n элементов, есть хотя бы одно множество, содержащее не менее 2-х элементов.
По традиции в популярной литературе принцип объясняется на примере "зайцев" и "клеток": "Если десять зайцев сидят в девяти клетках, то в некоторой клетке сидят не менее двух зайцев".
Для нащей задаче ящики - это "зайцы", а сорта - "клетки". 25 ящиков - "зайцев" рассадили по 3 - "клеткам"-сортам. Так как
то получим, что в каждой "клетке"-сорте не менее 9 "зайцев"-ящиков.
ответ: можно.
7.
т.е. только первый элемент множеств является общим, птому что если записать формулы всех элементов множеств начиная со второго, получаем
если приравнивать эти уравнения попарно друг другу, то общее решение будет при n=0, т.е. других общих элементов - нет.