Если подходить к задача строго, то обозначим
d - количество двухколесных велосипедов
t - количество трехколесных велосипедов
тогда количество рулей
d + t ≤ 15
тогда количество колес
2d + 3t ≤ 40
(знак неравенства используем потому, что могут остаться и неиспользованные рули и неиспользованные колеса в самом общем случае!)
умножаем первое неравенство на 2
2d + 2t ≤ 30
и вычитаем из второго
2d + 3t -(2d + 2t) ≤ 40-30
получим
t ≤ 10
вычитаем это неравенство из первого d + t ≤ 15, получим
d ≤ 5
таким образом, мы получили, что
наибольшее количество трехколесных велосипедов t = 10
наибольшее количество двухколесных велосипедов d = 5
при условии наиболее полного использования имеющихся деталей
и при условии наибольшего общего количества велосипедов
Пошаговое объяснение:
число п это отношение длины окружности к диаметру
п=С/d
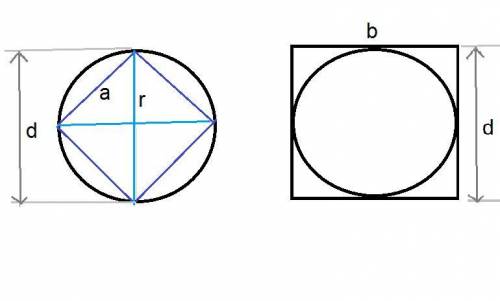
впишем в окружность квадрат и опишем около окружности квадрат
пусть периметр малого квадрата Р₁ периметр большого квадрата Р₂
1) рассмотрим малый квадрат
P₁=4a; d=2r
так как катет < гипотенузы то r<a; 4r<4a; 2d<4a; P₁=4a ; 2d<P₁
2) рассмотрим большой квадрат
b=d
P₂=4b=4d; P₂=4d;
длина окружности больше периметра малого квадрата и меньше периметра большого квадрата ⇒
P₁<С<P₂
2d<С<4d
разделим все на d
2<С/d<4 ; C/d=п ⇒
2<п<4
ответ:=-3-108c^2
Пошаговое объяснение:
(5+х)^2=25+10x+x^2;
(1-3)^2=1-6+9=4;
(3a-10b^2)=9a^2-60ab+100b^2;
(x^2+4)^2=x^4+8x^2+16;
4+4a+a^2=(2+a)^2;
a^2-8ab+16b^2=(a-4b)^2;
(2x-5)^2+20x=4x^2-20x+25+20x=4x^2+25;
36c-3(1+6c)^2=36c-3(1+12c+36c^2)=36c-3-36c-108c^2=-3-108c^2