Для начала вспомним, что тупой угол - это угол с градусной мерой больше 90° и меньше 180°. Из одной точки можно пустить три луча, которые между собой образуют 3 тупых угла.
Пустим 4-й луч вблизи одного из трёх лучей, у нас добавится дополнительно 2 тупых угла. 5-й луч пустим вблизи второго из числа первых трёх, дополнительно образуются 3 тупых угла. Наконец, пускаем 6-й луч вблизи третьего, получив дополнительно 4 тупых угла. У нас будет получаться как бы три пучка близко расположенных лучей в каждом пучке.
Считаем сколько получилось тупых углов после добаления к первым трём лучам ещё трёх лучей. 3 луча было, плюс 2, плюс 3 и плюс 4, всего 12 лучей.
Итак, для 3-х лучей - 3 тупых угла; для 6 лучей - 12 тупых углов.
Рассуждаем аналогично, добавляя по очереди ещё 3 луча. Добавятся сначало 4 угла, затем 5 и, наконец, 6; т.е. всего добавится 15 тупых углов. А всего для 9 лучей будет 27 тупых углов.
Точно также, считая для 12 лучей, получим дополнительно 6+7+8 = 21 тупых угла, а всего - 48.
Можно было бы и далее продолжать таким но мы замечаем закономерность.
Пусть а1 = 3 - это первый член последовательности. Используя предыдущее значение (рекуррентно), можно вычислить следующее значение по формуле: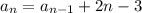
, где n - число лучей кратное 3.
Пробуем вычислить по этой формуле:
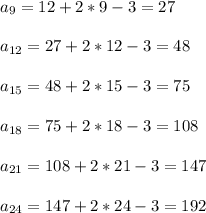
Итак, для 24 лучей возможно максимум 192 тупых угла.
136 = 2•2•2•17 или 8•17
40 = 2•2•2•5 или 8•5
Значит, размер наибольшего квадрата:
8 см х 8 см
2) Найдем количество квадратов с размерами 8 см х 8 см
По длине получается:
136:8=17 квадратов.
По ширине получается:
40:8=5 квадратов
Итого:
17•5 = 85 квадратов
ответ:
размеры наибольших квадратов
8 см х 8 см;
Всего таких квадратов получится 85 штук.
Проверка:
1) 136•40 = 5440 кв.см - площадь картонного листа.
2) 8•8= 64 кв.см - площадь одного наибольшего квадрата.
3) 5440:64= 85 целых квадратов получится.