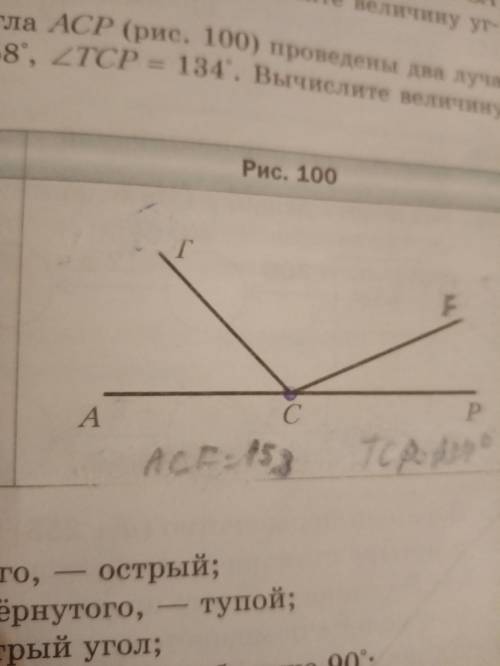
Задача имеет 2 решения. 1-ый вариант: когда основание треугольника > боковой стороны; 2-ой вариант: когда основание треугольника < боковой стороны.
36+44=81 см - периметр треугольника.
x см - основание треугольника.
((81-x)÷2)см - боковая сторона треугольника;
((81-x)÷4)см - 1/2 боковой стороны треугольника.
1 вариант:
x+ (81-x)/4 = 45 / ×4
4x + (81-x) = 45 × 4
3x+81=180
3x=99
x=33 см - основание треугольника
(81-33)÷2=24 см - боковая сторона треугольника.
ответ: основание треугольника 33 см, боковая сторона треугольника 24 см.
2 вариант:
x+(81-x)/4= 36 / ×4
4x+(81-x)=144
3x+81=144
3x=63
x=21 см - основание треугольника
(81-21)÷2= 30 см - боковая сторона треугольника.
ответ: основание треугольника 21 см, боковая сторона треугольника 30 см.
Пошаговое объяснение:
Для начала превратим смешанные числа в неправильные дроби. Для этого нужно целую часть умножить на знаменатель и прибавить к результату числитель. Знаменатель при этом не изменяется, а полученный результат идёт в числитель.
Теперь приведём дроби к общему знаменателю. Общий знаменатель — такое число, на которое делится знаменатель каждой дроби. В данном случае 15 делится на 5, поэтому 15 и будщет общим знаменателем. Ту дробь, у которой в знаменателе пять, мы домножаем на три: умножается и числитель, и знаменатель. Та дробь, у которой в знаменателе 15, не изменяется.
Остальные примеры решаются аналогично.
б)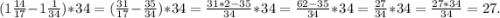
в)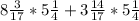
. Здесь имеет смысл 
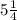вынести за скобки. Тогда получается: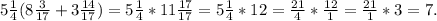 
г)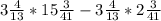
. Здесь аналогично.
д)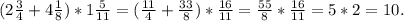
е)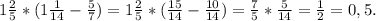
P. S. Сделано допущение, что в г) дробь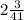
, а не 
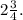В противном случае решается тяжело.