3 Вычисли письменно.
450 300
147 2 000
180 700
6 800 60
460 30
7 410 60
530 90
230 400

👇

Увидеть ответ

Ответ:

TemhenkoShasa

08.01.2023

1) ответ 135000

2)294000

4,5(91 оценок)

Открыть все ответы

Ответ:

nasamar

08.01.2023

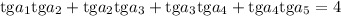
$\mathrm{tg}a_1\mathrm{tg}a_2+\mathrm{tg}a_2\mathrm{tg}a_3+\mathrm{tg}a_3\mathrm{tg}a_4+\mathrm{tg}a_4\mathrm{tg}a_5=4$

Выразим через третий член и разность прогрессии все остальные члены:

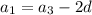
a_1=a_3-2d

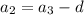
a_2=a_3-d

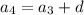
a_4=a_3+d

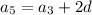
a_5=a_3+2d

Подставим получившиеся соотношения в уравнение:

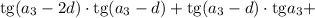
$\mathrm{tg}(a_3-2d)\cdot\mathrm{tg}(a_3-d)+\mathrm{tg}(a_3-d)\cdot\mathrm{tg}a_3+$

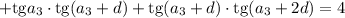
$+\mathrm{tg}a_3\cdot\mathrm{tg}(a_3+d)+\mathrm{tg}(a_3+d)\cdot\mathrm{tg}(a_3+2d)=4$

Применяем формулы тангенса суммы и тангенса разности:

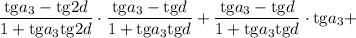
$\dfrac{\mathrm{tg}a_3-\mathrm{tg}2d}{1+\mathrm{tg}a_3\mathrm{tg}2d}\cdot\dfrac{\mathrm{tg}a_3-\mathrm{tg}d}{1+\mathrm{tg}a_3\mathrm{tg}d}+\dfrac{\mathrm{tg}a_3-\mathrm{tg}d}{1+\mathrm{tg}a_3\mathrm{tg}d}\cdot\mathrm{tg}a_3+$

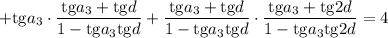
$+\mathrm{tg}a_3\cdot\dfrac{\mathrm{tg}a_3+\mathrm{tg}d}{1-\mathrm{tg}a_3\mathrm{tg}d}+\dfrac{\mathrm{tg}a_3+\mathrm{tg}d}{1-\mathrm{tg}a_3\mathrm{tg}d}\cdot\dfrac{\mathrm{tg}a_3+\mathrm{tg}2d}{1-\mathrm{tg}a_3\mathrm{tg}2d}=4$

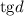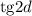Из имеющегося соотношения для разности прогрессии выразим величины $\mathrm{tg}d$ и $\mathrm{tg}2d$ :

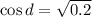
$\cos d=\sqrt{0.2}$

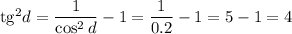
$\mathrm{tg}^2d=\dfrac{1}{\cos^2d} -1=\dfrac{1}{0.2} -1=5-1=4$

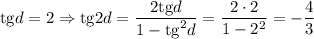
1) $\mathrm{tg}d=2\Rightarrow \mathrm{tg}2d=\dfrac{2\mathrm{tg}d}{1-\mathrm{tg}^2d} =\dfrac{2\cdot2}{1-2^2} =-\dfrac{4}{3}$

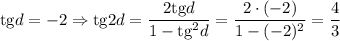
2) $\mathrm{tg}d=-2\Rightarrow \mathrm{tg}2d=\dfrac{2\mathrm{tg}d}{1-\mathrm{tg}^2d} =\dfrac{2\cdot(-2)}{1-(-2)^2} =\dfrac{4}{3}$

Первый случай: 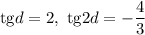$\mathrm{tg}d=2,\ \mathrm{tg}2d=-\dfrac{4}{3}$

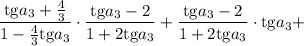
$\dfrac{\mathrm{tg}a_3+\frac{4}{3} }{1-\frac{4}{3}\mathrm{tg}a_3}\cdot\dfrac{\mathrm{tg}a_3-2}{1+2\mathrm{tg}a_3}+\dfrac{\mathrm{tg}a_3-2}{1+2\mathrm{tg}a_3}\cdot\mathrm{tg}a_3+$

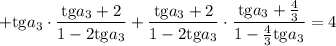
$+\mathrm{tg}a_3\cdot\dfrac{\mathrm{tg}a_3+2}{1-2\mathrm{tg}a_3}+\dfrac{\mathrm{tg}a_3+2}{1-2\mathrm{tg}a_3}\cdot\dfrac{\mathrm{tg}a_3+\frac{4}{3} }{1-\frac{4}{3}\mathrm{tg}a_3}=4$

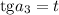
Замена: $\mathrm{tg}a_3=t$

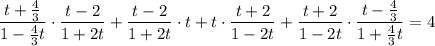
$\dfrac{t+\frac{4}{3} }{1-\frac{4}{3}t}\cdot\dfrac{t-2}{1+2t}+\dfrac{t-2}{1+2t}\cdot t+t\cdot\dfrac{t+2}{1-2t}+\dfrac{t+2}{1-2t}\cdot\dfrac{t-\frac{4}{3} }{1+\frac{4}{3}t}=4$

Числитель и знаменатель первой и последней дроби умножим на 3:

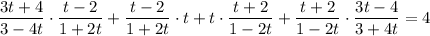
$\dfrac{3t+4 }{3-4t}\cdot\dfrac{t-2}{1+2t}+\dfrac{t-2}{1+2t}\cdot t+t\cdot\dfrac{t+2}{1-2t}+\dfrac{t+2}{1-2t}\cdot\dfrac{3t-4}{3+4t}=4$

Складываем первые два слагаемых левой части уравнения:

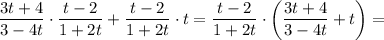
$\dfrac{3t+4}{3-4t}\cdot\dfrac{t-2}{1+2t}+\dfrac{t-2}{1+2t}\cdot t=\dfrac{t-2}{1+2t}\cdot\left(\dfrac{3t+4}{3-4t}+t\right)=$

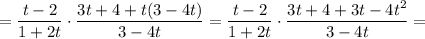
$=\dfrac{t-2}{1+2t}\cdot\dfrac{3t+4+t(3-4t)}{3-4t}=\dfrac{t-2}{1+2t}\cdot\dfrac{3t+4+3t-4t^2}{3-4t}=$

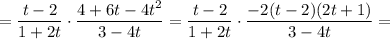
$=\dfrac{t-2}{1+2t}\cdot\dfrac{4+6t-4t^2}{3-4t}=\dfrac{t-2}{1+2t}\cdot\dfrac{-2(t-2)(2t+1)}{3-4t}=$

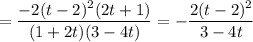
$=\dfrac{-2(t-2)^2(2t+1)}{(1+2t)(3-4t)}=-\dfrac{2(t-2)^2}{3-4t}$

Складываем последние два слагаемых левой части уравнения:

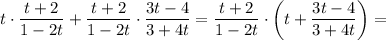
$t\cdot\dfrac{t+2}{1-2t}+\dfrac{t+2}{1-2t}\cdot\dfrac{3t-4}{3+4t}=\dfrac{t+2}{1-2t}\cdot\left(t+\dfrac{3t-4}{3+4t}\right)=$

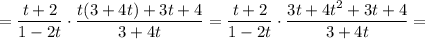
$=\dfrac{t+2}{1-2t}\cdot\dfrac{t(3+4t)+3t+4}{3+4t}=\dfrac{t+2}{1-2t}\cdot\dfrac{3t+4t^2+3t+4}{3+4t}=$

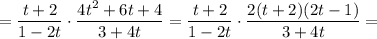
$=\dfrac{t+2}{1-2t}\cdot\dfrac{4t^2+6t+4}{3+4t}=\dfrac{t+2}{1-2t}\cdot\dfrac{2(t+2)(2t-1)}{3+4t}=$

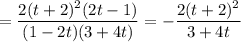
$=\dfrac{2(t+2)^2(2t-1)}{(1-2t)(3+4t)}=-\dfrac{2(t+2)^2}{3+4t}$

Складываем две получившиеся в предыдущих пунктах величины:

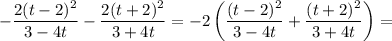
$-\dfrac{2(t-2)^2}{3-4t}-\dfrac{2(t+2)^2}{3+4t}=-2\left(\dfrac{(t-2)^2}{3-4t}+\dfrac{(t+2)^2}{3+4t}\right)=$

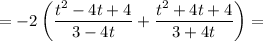
$=-2\left(\dfrac{t^2-4t+4}{3-4t}+\dfrac{t^2+4t+4}{3+4t}\right)=$

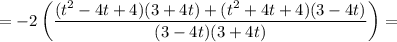
$=-2\left(\dfrac{(t^2-4t+4)(3+4t)+(t^2+4t+4)(3-4t)}{(3-4t)(3+4t)}\right)=$

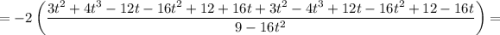
$=-2\left(\dfrac{3t^2+4t^3-12t-16t^2+12+16t+3t^2-4t^3+12t-16t^2+12-16t}{9-16t^2}\right)=$

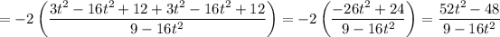
$=-2\left(\dfrac{3t^2-16t^2+12+3t^2-16t^2+12}{9-16t^2}\right)=-2\left(\dfrac{-26t^2+24}{9-16t^2}\right)=\dfrac{52t^2-48}{9-16t^2}$

Тогда, уравнение примет вид:

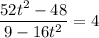
$\dfrac{52t^2-48}{9-16t^2}=4$

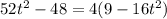
52t^2-48=4(9-16t^2)

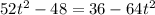
52t^2-48=36-64t^2

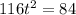
116t^2=84

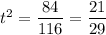
$t^2=\dfrac{84}{116} =\dfrac{21}{29}$

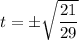
$t=\pm\sqrt{\dfrac{21}{29} }$

Обратная замена: 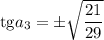$\mathrm{tg}a_3=\pm\sqrt{\dfrac{21}{29} }$

Находим требуемую величину:

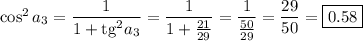
$\cos^2 a_3=\dfrac{1}{1+\mathrm{tg}^2a_3} =\dfrac{1}{1+\frac{21}{29} } =\dfrac{1}{\frac{50}{29} } =\dfrac{29}{50} =\boxed{0.58}$

Второй случай: 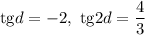$\mathrm{tg}d=-2,\ \mathrm{tg}2d=\dfrac{4}{3}$

Заметим, что при подстановке этих значений в уравнение, получится такое же уравнение, как и в предыдущем случае с той лишь разницей, что первое и четвертое, а также второе и третье слагаемое будут поменяны местами. Значит, никаких новых результатов получено не будет.

ответ: 0.58

4,7(47 оценок)

Ответ:

Ольга1738

08.01.2023

Рассмотрим максимальное число победных игр: 75 : 3 = 25 (игр), но при таком варианте игр вничью быть не может.

Будем уменьшать число победных игр и считать, сколько за это команда получит очков. Предположим, что победных игр 24: 24 · 3 = 72. Таким образом, в данной конфигурации может быть 24 победы, 3 поражения и 3 ничьи.

Предположим, что победных игр 23: 23 · 3 = 69. Получаем, что 6 очков за ничью и 0 очков за поражение.

Предположим, что победных игр 22: 22 · 3 = 66. Получаем, что такой ситуации быть не может, так как максимальное число игр вничью — восемь, следовательно, 8 очков — 66 + 8 = 74, а в условии сказано, что команда набрала 75 очков.

Таким образом, наибольшее число ничейных матчей — 6.

4,6(38 оценок)

Это интересно:

Искусство-и-развлечения

07.05.2022

Как играть на тромбоне: советы и рекомендации для начинающих...

12.09.2020

Как остановить человека, который задирает вас...

Компьютеры-и-электроника

26.04.2020

Как изменить одежду сима в The Sims 2: простые шаги...

Компьютеры-и-электроника