Сумма цифр числа (n-1) равна
41 + 9•kгде k - количество нулей, стоящих на конце числа n
Пошаговое объяснение:
Оу! попробуем.
Итак, есть некое число
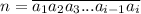
причем такое, что сумма его цифр равна 42.
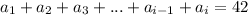
Обратим внимание, что ноли на конце этого числа n не оказывают влияния на сумму его цифр.
При вычитании единицы из n запись числа может принять следующие варианты:
а)
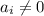
Уменьшается последняя цифра числа на единицу, остальные цифры не изменяются. Сумма цифр будет следующей:
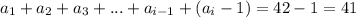
б)
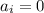
Сумма цифр будет выглядеть:
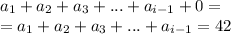
так как ноли на конце этого числа n не оказывают влияния на сумму его цифр.
Последняя цифра обращается в "9", предыдущая цифра уменьшается на единицу. Сумма цифр будет следующей:
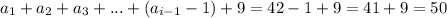
в) Несколько последних цифр (пусть, k цифр)- нули.
Число можно представить как
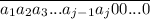
где а(j) - крайняя справа отличная от нуля цифра.
Сумма цифр будет выглядеть:
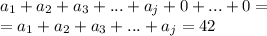
Количество нулей в этой записи равно k шт.
При вычитании единицы все эти нули на конце числа превращаются в "9". Девяток будет ровно столько же, сколько было нулей, т.е. k шт.
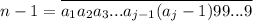
Сумма цифр для n-1 будет равна:
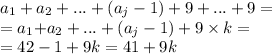
ОБОБЩЕНИЕ:
Все случаи можно отобразить одной формулой:
Сумма цифр числа
(n-1)
равна
41 + 9•kгде k - число нулей, стоящих на конце числа n