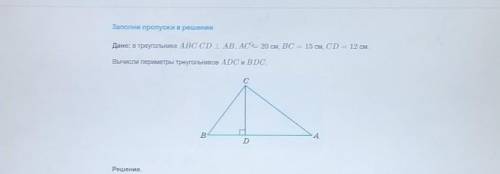
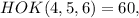
 где
где  – некоторое целое число.
– некоторое целое число.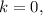 тогда
тогда 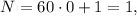 но
но  не делится на
не делится на  а значит не подходит.
а значит не подходит.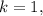 тогда
тогда 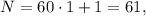 но
но 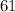 не делится на
не делится на  а значит не подходит.
а значит не подходит. тогда
тогда 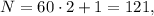 но
но 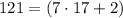 не делится на
не делится на  а значит не подходит.
а значит не подходит.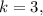 тогда
тогда 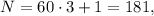 но
но 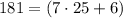 не делится на
не делится на  а значит не подходит.
а значит не подходит.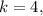 тогда
тогда 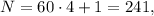 но
но 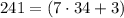 не делится на
не делится на  а значит не подходит.
а значит не подходит. тогда
тогда 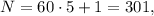 и
и 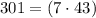 – делится на
– делится на  а значит подходит !
а значит подходит !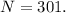
 где
где  – некоторое целое число.
– некоторое целое число.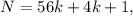 где
где  – некоторое целое число.
– некоторое целое число.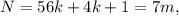 где
где  и
и 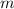 – некоторые целые числа.
– некоторые целые числа.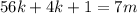 ;
;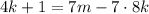 ;
;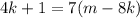 – правая часть здесь кратна семи, а значит и левая кратная семи, т.е.:
– правая часть здесь кратна семи, а значит и левая кратная семи, т.е.: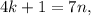 где
где  и
и  – некоторые целые числа.
– некоторые целые числа.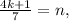 где
где  и
и  – некоторые целые числа.
– некоторые целые числа. а значит:
а значит: где
где 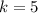 ;
;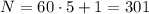 ;
; где
где  – некоторое целое число.
– некоторое целое число.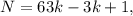 где
где  – некоторое целое число.
– некоторое целое число. где
где  и
и 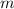 – некоторые целые числа.
– некоторые целые числа.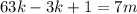 ;
;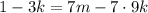 ;
;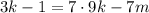 ;
;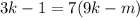 – правая часть здесь кратна семи, а значит и левая кратная семи, т.е.:
– правая часть здесь кратна семи, а значит и левая кратная семи, т.е.: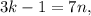 где
где  и
и  – некоторые целые числа.
– некоторые целые числа.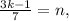 где
где  и
и  – некоторые целые числа.
– некоторые целые числа. а значит:
а значит: где
где 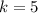 ;
;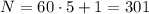 ;
;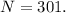
ответ:
пошаговое объяснение: сказка о дробях № 1
жили два брата. одного звали числитель, а другого знаменатель. дружба у них была крепкая. когда они были вместе, их все звали дробью. жить один без другого они не могли. однажды пошли они в лес. в лесу были две дорожки. одна вела направо, а другая налево. и разошлись братья по разным тропинкам, но договорились встретиться у ручья. по дороге числитель встретил старика, которого звали деление. они разговорились:
- дай мне воды, внучок, я тебя . а за это я тебе путь покажу легче.
дал числитель воды делению. а старик так и сделал. он разделил числитель. то же самое произошло и со знаменателем. вскоре они встретились у ручья и соединились. старик не обманул, он показал правило сокращения дроби и жить братьям стало интереснее и легче.
сказка о дробях № 2
жила-была королева дробей единица. и жили в ее стране разные дроби. единица решила, что каждая дробь, у которой числитель меньше знаменателя будет называться правильной дробью, а у которой числитель больше или равен знаменателю – неправильной. и еще увидела она, что есть дроби, у которых числитель и знаменатель можно разделить на одно и то же число. и назвала анна это действие сокращением дробей. так и правит королева дробей своей страной.