Пошаговое объяснение:
Чтобы привести дроби к наименьшему общему знаменателю, нужно подобрать такие числа, при умножении которых в знаменателе мы получим одинаковое число:
а) 5/8 = 5×4/8×4= 20/32
9/16=9×2/16×2= 18/32
б) 5/12=5×3/12×3= 15/36
11/18=11×2/18×2=22/36
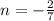 - знаменатель обращается в 0.
- знаменатель обращается в 0.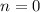 - по обычаю проверяется эта точка.
- по обычаю проверяется эта точка. (при
(при  →∞)
→∞)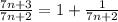

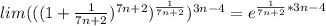 (при
(при  →∞)
→∞)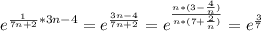 (при
(при  →∞)
→∞) →+∞ предел равен
→+∞ предел равен 
 →-∞ предел равен
→-∞ предел равен 
 →0 предел равен:
→0 предел равен:
 →
→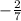
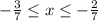 - мы получаем отрицательное основание).
- мы получаем отрицательное основание).
1)16
2)18
если что пиши в личку