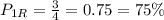 ;
;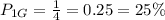 ;
;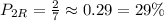 ;
;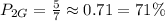 ;
;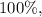 а достают зелёный с долей
а достают зелёный с долей 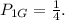 Общая вероятность плохого предсказания составит тут
Общая вероятность плохого предсказания составит тут 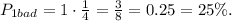
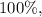 а достают красный с долей
а достают красный с долей 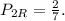 Общая вероятность плохого предсказания составит тут
Общая вероятность плохого предсказания составит тут 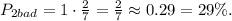
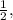 а достают зелёный с долей
а достают зелёный с долей 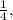 или наоборот, предсказывают зелёный с долей
или наоборот, предсказывают зелёный с долей 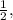 а достают красный с долей
а достают красный с долей 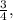 Общая вероятность плохого предсказания составит тут
Общая вероятность плохого предсказания составит тут 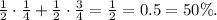
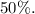
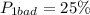 ошибок в первом случае, и
ошибок в первом случае, и 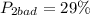 ошибок во втором случае, поэтому угадывание цвета доставаемого шара менее предсказуемо во втором случае.
ошибок во втором случае, поэтому угадывание цвета доставаемого шара менее предсказуемо во втором случае.
Пошаговое объяснение:
Решение: всего в урне: 4 + 7 = 11 шаров. Поехали:
а) Рассмотрим события – первый шар будет белым, – второй шар будет белым и найдём вероятность события , состоящего в том, что 1-й шар будет белым и 2-й белым.
По классическому определению вероятности: . Предположим, что белый шар извлечён, тогда в урне останется 10 шаров, среди которых 3 белых, поэтому:
– вероятность извлечения белого шара во 2-м испытании при условии, что до этого был извлечён белый шар.
По теореме умножения вероятностей зависимых событий:
– вероятность того, что оба шара будут белыми.