Найди значения выражений удобным для тебе вот выражения) : (58+37)-28 ( по з выражения , 26+(14+31) - id148794320230120 от pollyj 20.01.2023 19:58

Question

Математика: Найди значения выражений удобным для тебе вот выражения) : (58+37)-28 ( по з выражения , 26+(14+31) тоже 3 выражения , (48+13)+27 3 выражения (46+69)-39тоже 3выражния

pollyj · Accepted Answer

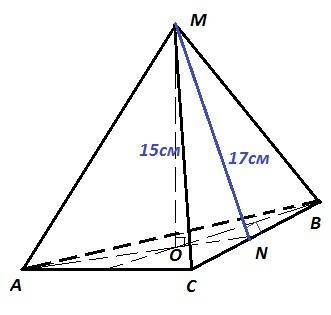
Дано : MABC - правильная пирамида. h = MO = 15 см - высота пирамиды. L = MN = 17 см - апофема.

Площадь боковой поверхности пирамиды равна произведению полупериметра основания на апофему : S = pL

ΔMON - прямоугольный. Теорема Пифагора

ON² = MN² - MO² = 17² - 15² = (17-15)(17+15)=2·32 = 64 = 8²

ON = 8 см

Высота правильной пирамиды опускается в центр окружности, вписанной в равносторонний треугольник основания ⇒

r = ON = 8 см и 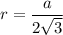$r = \dfrac a{2\sqrt 3}$ ⇒

AB = CB = AC = a = r · 2√3 = 8 · 2√3 = 16 √3 см

Площадь боковой поверхности пирамиды

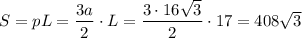$S = pL = \dfrac{3a}{2}\cdot L = \dfrac{3\cdot16\sqrt 3}{2}\cdot 17 = 408\sqrt 3$ см²

ответ : 408√3 см²

Висота правильної трикутної піраміди 15 см, а апофема піраміди - 17 см. знайти площу бічної поверхні

Найди значения выражений удобным для тебе вот выражения) : (58+37)-28 ( по з выражения , 26+(14+31) тоже 3 выражения , (48+13)+27 3 выражения (46+69)-39тоже 3выражния

MOGZ ответил