Раз поросенок весит столько, сколько 4 кошки, то 2 кошки и поросенок - это все равно что полтора поросенка.
Раз полтора поросенка = 3 учебнникам, то один поросенок (а, значит, и четыре кошки) весят как 2 учебника.
Вот и все:
Из 5 учебников в начале загадки два приходились на поросенка, а три на ребенка.
Значит "в кошках" вес ребенка равен шести!))
1 ребенок = 6 кошек.
То ли кошки такие упитанные, то ли ребенок худой и мелкий))
![\left[\begin{array}{ccc}3x&5y&7z\\2x&-1y&0?\\4x&3y&2z\end{array}\right]](/tpl/images/0826/6006/67d9d.png) (x, y, z написал для наглядности)..
(x, y, z написал для наглядности).. ![\left[\begin{array}{ccc}1\\2\\-1\end{array}\right]](/tpl/images/0826/6006/6a2b2.png)
![\left[\begin{array}{ccc}1&5&7\\2&-1&0\\-1&3&2\end{array}\right]](/tpl/images/0826/6006/88770.png)
![\left[\begin{array}{ccc}3&1&7\\2&2&0\\4&-1&2\end{array}\right]](/tpl/images/0826/6006/0df2a.png)
![\left[\begin{array}{ccc}3&5&1\\2&-1&2\\4&3&-1\end{array}\right]](/tpl/images/0826/6006/f8d8c.png)

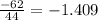
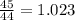
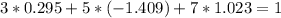
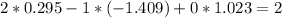
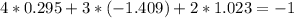
![\left[\begin{array}{ccc}3x&5y&7z\\2x&-1y&0?\\4x&3y&2z\end{array}\right]](/tpl/images/0826/6006/67d9d.png) (x, y, z написал для наглядности)..
(x, y, z написал для наглядности).. ![\left[\begin{array}{ccc}1\\2\\-1\end{array}\right]](/tpl/images/0826/6006/6a2b2.png)
![\left[\begin{array}{ccc}1&5&7\\2&-1&0\\-1&3&2\end{array}\right]](/tpl/images/0826/6006/88770.png)
![\left[\begin{array}{ccc}3&1&7\\2&2&0\\4&-1&2\end{array}\right]](/tpl/images/0826/6006/0df2a.png)
![\left[\begin{array}{ccc}3&5&1\\2&-1&2\\4&3&-1\end{array}\right]](/tpl/images/0826/6006/f8d8c.png)

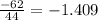
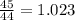
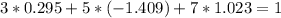
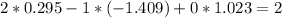
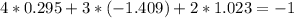
Р - ребенок,
П - поросенок
К - кошка
У - учебник
СИСТЕМА: Р+П=5У (1)
П=4К (2)
2К+П=3У (3)
Из (3) вычислим 1 учебник: 3У=2К-П
У=(2К+П)/3
Из (1) вычислим ребенка: Р=5У-П.
Так как П=4К, получаем : Р=5У-4К
Вместо чеников подставляем : Р=5((2К+П)/3)-4К
Решаем, заменив поросенка на 4 котенка:
Р=5((2К+4К)/3)-4К
Р=5(6К/3)-4К
Р=5*2К-4К
Р=10К-4К
Р=6К
ответ. 6 кошек уравновесят одного ребенка