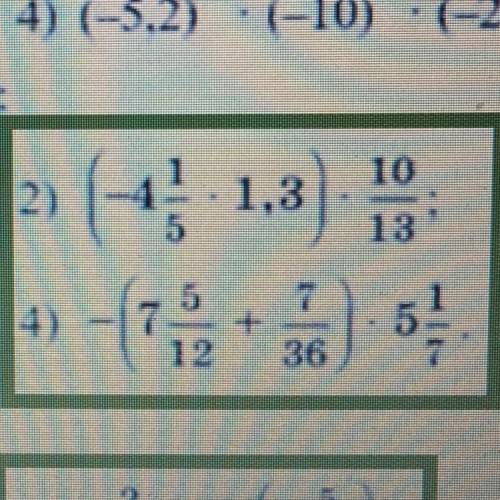
Пошаговое объяснение:
1 Проведите прямую, обозначьте ее буквой а и отметьте точки A и B, лежащие на этой прямой, и точки Р, Q и R, не лежащие на ней. Опишите взаимное расположение точек А, В, Р, Q, R и прямой а, используя символы ∈ и ∉.
2 Отметьте три точки A, B и C, не лежащие на одной прямой, и проведите прямые AB, BC и CA.
3 Проведите три прямые так, чтобы каждые две из них пересекались. Обозначьте все точки пересечения этих прямых. Сколько получилось точек? Рассмотрите все возможные случаи.
4 Отметьте точки A, B, C, D так, чтобы точки A, B, C лежали на одной прямой, а точка D не лежала на ней. Через каждые две точки проведите прямую. Сколько получилось прямых?
5 Проведите прямую а и отметьте на ней точки A и B. Отметьте: а) точки М и N, лежащие на отрезке АВ; б) точки Р и Q, лежащие на прямой а, но не лежащие на отрезке АВ; в) точки R и S, не лежащие на прямой а.
6 Проведите прямую и отметьте на ней три точки. Сколько отрезков получилось на прямой?
7 На рисунке 10 изображена прямая, на ней отмечены точки А, В, С и D. Назовите все отрезки: а) на которых лежит точка С; б) на которых не лежит точка B.
Пошаговое объяснение:
9)
1)RS²=400+225
RS=25
sin∠R=20/25=4/5=0.8
cos∠R=15/25=3/5=0.6
tg∠R=20/15=4/3=1 1/3
sin∠S=15/25=3/5=0.6
cos∠S=20/25=4/5=0.8
tg∠S=15/20=3/4=0.75
2)BC²=100-36
BC=8
sin∠B=6/10=3/5=0.6
cos∠B=8/10=4/5=0.8
tg∠B=6/10=3/5=0.6
sin∠A=8/10=0.8
cos∠A=6/10=0.6
tg∠A=8/6=4/3=1 1/3
3)XY²=4+9
XY=√13
sin∠X=3/√13=3√13/13
cos∠X=2/√13=2√13/13
tg∠X=3/2=1.5
sin∠Y=2/√13=2√13/13
cos∠Y=3/√13=3√13/13
tg∠Y=2/3
4)DH²=25-1
DH=2√6
sin∠G=2√6/√5=2√30/5
cos∠G=1/√5=√5/5
tg∠G=2√6/1=2√6
sin∠H=1/√5=√5/5
cos∠H=2√6/√5=2√30/5
tg∠H=1/2√6=√6/12
10)CB²=100+36
CB=2√34
6/sin∠ABC=10/sin∠ACB
sin∠ABC=x
6/x=10
10x=6
x=6/10
x=0.6
sin∠ABC≈37°
∠CAB≈180-90-37
∠CAB≈53°
∠TAC≈53/2≈26°
∠ATC≈180-90-26
∠ATC≈64°
6/sin∠64°=AT/sin∠ACT
AT=x
60/9=x
x=20/3
x=6 2/3
CT²=400/9-36
CT²=(400-324)/9
CT²=76/9
CT=2√19/3
sin∠TAC=2√19/3÷6 2/3
sin∠TAC=√19/10
cos∠TAC=6÷6 2/3=(6*3)/20=18/20=9/10=0.9
tg∠TAC=2√19/3÷6=2√19/18=√19/9
1. -4,2
2. 1 целая 1/7