ответ: b = (-3,6,6), b (3; -6; -6), α = -60⁰
Пошаговое объяснение:
Дан вектор a(-1;2;2). Найдите координаты вектора b, коллинеарного вектору a, если a·b = 27.
Скалярное произведение векторов а и b определяется как произведение длин этих векторов на косинус угла между ними!
Поскольку векторы коллинеарные, то угол между ними равен 0 градусов, т. е косинус угла равен 1.
Длина вектора a равна
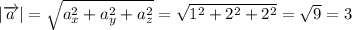
По условию задания скалярное произведение векторов равно 27
Зная длину вектора а найдем длину вектора b
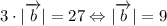
Поскольку вектора а и b коллинеарны, то и координаты связаны уравнением
Подставим координаты вектора а
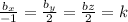
Запишем координаты вектора b через новую переменную k bx = -k, by =2k, bz = 2k
b = (-k,2k,2k)
Определим длину вектора и по теореме Пифагора
Так как длину вектора b мы знаем из скалярного произведения то
3|k| = 9
k₁ = 3 k₂=-3
Получили два варианта вектора b
Для k = 3
b = (-3,6,6)
Для k = -3
b (3; -6; -6)
Найдем угол между векторами a и c из формулы скалярного произведения, если a*c = -6; c = 4
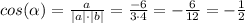
α = arccos(-0,5) = -60⁰
Давным-давно, вовсе не в тридевятом царстве и не в тридесятом королевстве, а в нашем родном с вами городе, когда еще не было высоких домов и шумных автомобилей, возвышалась большая Высокая гора. Сейчас на этом месте располагается Юбилейная площадь. Но раньше эту гору люди называли Змеевой. Да-да, вы правильно догадались, в ее глубоких пещерах жил страшный огнедышащий змей, он же кровожадный дракон. Дракон, как это и принято среди всех уважающих себя злых сказочных существ, нападал на местных жителей. Испуская дым и огонь, он летал по округе, приводя людей в трепетный ужас. Требовал дань, различные яства и сокровища, похищал людей. А раз в год заставлял окрестные селения предоставлять ему в жертву десять красивых девушек. Красавиц, идущих на заклание, выбирали по жребию. Но в один несчастливый для дракона день выбор жребия пал на девушку, суженым которой был известный местный богатырь.