3.9×4=15.6
4.3×4=17.2
найдём производную функции f(x)=2x³ -3x² -1
f'(x)=6x² - 6x
6x² - 6x= 0
6x(x -1) = 0
1) 6x = 0
x₁ = 0
2) x -1=0
x₂ = 1
график функции f'(x)=6x² - 6x представляет собой квадратную параболу веточками ввех, следовательно,
при х∈(-∞; 0] f'(x)> 0 ⇒ f(x) возрастает
при х∈[0; 1] f'(x)< 0 ⇒ f(x) убывает
при х∈[1; +∞) f'(x)> 0 ⇒ f(x) возрастает
в точке х = 0 локальный максимум y mах = -1
в точке х =1 локальный минимум y min = 2 -3 -1 = -2
Пошаговое объяснение:
касательная АВ. точка касания В; АО1 = О1В; ∠ ВАС - обозначим ∠α
теперь
АО = ОС (это из того, что ОО1 средняя линия ΔАВС)
ОА = ОС = х; ВС = у
ВС/АС = tg α и поскольку АВ касательная, то это у'
т.е.
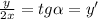
дальше решаем дифференциальное уравнение
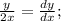
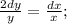 ⇒
⇒ 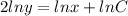 ⇒
⇒ 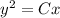
получилась парабола.
если бы была какая-нибудь точка, через которую парабола проходит, то можно было бы написать точное уравнение.
а так ответ такой
отрезок любой касательной, заключенный между точкой касания и осью абсцисс делится осью ординат пополам у параболы
Периметр 1 - 15,6 сторона 3,9, периметр 2 - 17,2 сторона 4,3