Пошаговое объяснение:
сли при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны
Пусть при пересечении прямых а и b секущей АВ накрест лежащие углы равны. Например, ∠ 4 = ∠ 6. Докажем, что а || b.
Предположим, что прямые а и b не параллельны. Тогда они пересекаются в некоторой точке М и, следовательно, один из углов 4 или 6 будет внешним углом треугольника АВМ. Пусть для определенности ∠ 4 — внешний угол треугольника АВМ, а ∠ 6 — внутренний. Из теоремы о внешнем угле треугольника следует, что ∠ 4 больше ∠ 6, а это противоречит условию, значит, прямые а и 6 не могут пересекаться, поэтому они параллельны.
Решение
7. sinx - чентая функция, поэтому площади под графиком слева и справа будут равны по модулю, но противоположны по знаку. Примем эту площадь за a: a + (-a) = 0 ответ: А.
8. Аналогично f(x)=x - четная функция. ответ: В.
9. Абсолютно то же самое: если функцию переместить на 1 влево, то нужно будет находить интеграл от -1 до 1 функции f(x) = x. ответ: А.
10. площадь фигуры равна -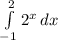
ответ: А.
11. Небходимо сравнить площади под графиками от a до b. Очевидно, что площадь под f больше, чем под g. ответ: Б.
12. Выделенная площадь - разность площади под графиком
и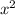 
, а по свойствам интегралов их разность равная интегралу разницы функций (если области совпадают, конечно, а унас именно так и есть). ответ: Г.