1){2x+7y-44=0
{2x-3y=-36
2x+7y=44. | -
2x-3y=-36
-2x-7y=-44
2x-3y=-36
-10y=-80
y=8
ПОДСТАВЛЯЕМ ЗНАЧЕНИЕ У В ОДНО ИЗ УРАВНЕНИЙ2x-3y=-36
2х-3×8=-36
2х-24=-36
2х=-36+24
2х=-12
х=-6
(-6;8)2){х-8у-17=0
{3х+4у-23=0
{х-8у=17
{ 3х+4у=23 |2
{х-8у=17
{6х+8у=46
7х=63
х=9
ПОДСТАВЛЯЕМ ЗНАЧЕНИЕ Х В ОДНО ИЗ УРАВНЕНИЙ:х-8у=17
9-8у=17
-8у=17-9
-8у=8
у=-1
(9;-1)Пошаговое объяснение:
экстремумы ищем при первой производной
y' = 3x²+6x = 3x(x+2)
приравняем ее к 0
3x(x+2) = 0 ⇒ х₁ =0 х₂ =-2 -это критические точки, т.е. точки возможных локальных экстремумов
теперь, по правилам, надо исследовать эти точки при достаточного условия экстремума функции
вторая производная
y'' = 6x+6
посмотрим на знаки второй производной в критических точках
y''(0) = 6>0 - точка x₁ = 0 это точка минимума y(0) = -4
y''(-2) = -6<0 - точка x₂ = -2 это точка максимума y(-2) = 0.
ответ
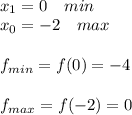
для проверки посмотрим график функции

1)умножаем второе уравнение на минус единицу и складываем с первым, получим
2х+7у-44=0
-2х+3у=36
10у=44+36
у=8. х=(-36+3*8)/2; х=-6
ответ (-6;8)
2)х-8у-17=0
3х+4у-23=0
умножим первое уравнение на минус три и сложим со вторым
-3х+24у=-51=
3х+4у=23
28у=-28
у=-1
х=17+8*(-1); х= 9
ответ (9; -1)