
5 см
Пошаговое объяснение:
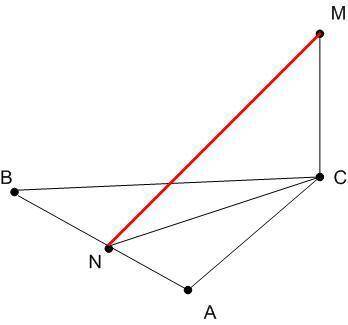
IACI=IBCI по условию, как стороны равнобедренного треугольника.
Построим отрезок СN такой, что IANI=IBNI. Отрезок CN является одновременно медианой, высотой и биссектрисой, опущенной на основание равнобедренного треугольника. Следовательно ∠CNA = ∠CNB = 90° (по определению высоты, опущенной из вершины на основание), и IANI=IBNI (по определению медианы).
Плоскость ΔMNC перпендикулярна отрезку AB, т.к. AB ⊥CN (определение: прямая перпендиклярна плоскости, если она перпендикулярна любой прямой, принадлежащей плоскости), следователно и MN ⊥ AB.
Следовательно длина отрезка IMNI и есть расстояние от точки M до стороны (отрезка) AB (определение: расстояние от точки до плоскости есть длина перпендикуляра, опущенного из точки на плоскость).
Найдем длину отрезка MN:
1. Сначала найдем длину ICNI:
ICNI=√(IBCI² - INBI²);
ICNI=√(5²-4²)=√9=3;
2. А теперь найдем IMNI из ΔMNC:
IMNI=√(ICNI²+ICMI²);
IMNI=√(3²+4²)=√25=5 (см)
1) Обе открыты, 2) левая открыта, 3) правая открыта,
4) обе закрыты.
Если обе открыты, то можно поставить 2 горшка.
Тогда сигналов при открытых занавесках будет 7:
1) цветов нет, 2) на левой цветок 1, 3) на левой цветок 2,
4) на правой цветок 1, 5) на правой цветок 2,
6) 2 цветка, слева 1, справа 2, 7) 2 цветка, слева 2, справа 1.
Если левая открыта, на ней может стоять один или другой,
или никакой - 3 сигнала.
Тоже самое на правой стороне - 3 сигнала.
Если обе занавески закрыты, то цветов нет - 1 сигнал.
Таким образом, получается 7 + 3 + 3 + 1 = 14 сигналов.
Значит, для 16 сигналов нужен еще третий цветок.
ответ: 3 цветка.