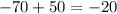
Пошаговое объяснение:
1 Частные производные для F(x,y,z)=1
dFx=2x, dFy=-2y, dFz=-2z
Значения частных производных в заданной точке - это координаты вектора нормали для касательной плоскости N=(2,4,-4)
Уравнение плоскости A*x+B*y+C*z+D=0
A=Nx=2 B=Ny=4 C=Nz=-4
D=-(Nx*Mx+Ny*My+Mz*Mz)=-(2*1+4*(-2)+(-4)*2)=14
Плоскость 2x+4y-4z+14=0
Нормаль (x-1)/2=(y+2)/4=(2-z)/4
2 Частные производные для F(x,y,z)=2
dFx=2xz-2y^3, dFy=-6xy^2, dFz=12z^3+x^2
Значения частных производных в заданной точке - это координаты вектора нормали для касательной плоскости N=(0,-6,13)
Уравнение плоскости A*x+B*y+C*z+D=0
A=Nx=0 B=Ny=-6 C=Nz=13
D=-(Nx*Mx+Ny*My+Mz*Mz)=-(0*1+(-6)*1+13*1)=-7
Плоскость -6y+13z-7=0
Нормаль (1-y)/6=(z-1)/13
3. Производные на вложенном изображении.
Чтобы перейти к целым числам значения производных в т (1,1,1) домножены на 6.
Вектор нормали тогда N=(3,5,38)
Уравнение плоскости 3x+5y+38z-46=0
Нормаль (x-1)/3=(y-1)/5=(z-1)/38

ответ:
пошаговое объяснение:
1
1) (-∞; 0)∪(0; +∞)
2) (-∞; 3)∪(3; +∞)
3) (-∞; 7)∪(7; +∞)
4) (-∞; 0)∪(0; +∞)
5) (-∞; 1)∪(1; +∞)
6) (-∞; -4)∪(-4; 4)∪(4; +∞)
7) (-∞; -11)∪(-11; 2)∪(2; +∞)
2
1)=2/3
2)=b/c
3)=b/c
4)=b/y
5)=((a(a-b))/ac=(a-b)/c
6)=((a(a-b))/((a(a+b))=(a-b)/(a+c)
7)аналогично
8)аналогично
9)аналогично
10)=((x-1)(x+1))/((x(x-1))=(x+1)/x
11)=x^2/((x(x+1))=x/(x+1)
12)также как и 10
13)=1/m
14)=(a-3b)/((a-3b)(a+3b)=1/(a+3b)
15)=p
16)=так же как и 14
17)=((a-b)^2)/(a-b)=a-b
18)далее аналогично
ответ на данное задание
-70+50=-20