Среди этих чисел не может быть числа, оканчивающегося на 0, так как на 0 не делится никакое число.
Значит, эти числа либо от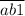 
до 
, либо от 
до 
.
Значит, в любом случае среди этих чисел есть следующие:
, делящееся на 2
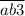, делящееся на 3
, делящееся на 4
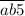, делящееся на 5
, делящееся на 6
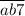, делящееся на 7
, делящееся на 8
Рассмотрим утверждение "" делится на 4"". Число делится на 4, если число, образованное двумя последними цифрами делится на 4. Значит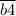 
делится на 4, 
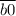делится на 4, 
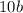делится на 4, 
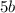делится на 2, значит 
- четное.
Рассмотрим утверждение ""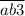 делится на 3"". Число делится на 3, если сумма цифр числа делится на 3. Значит, 
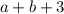делится на 3, 
делится на 3. Выпишем пары цифр, где 
, а - четное, в сумме кратные 3: (1; 2); (1; 8); (2; 4); (3; 0); (3; 6); (4; 2); (4; 8); (5; 4); (6; 0); (6; 6); (7; 2); (7; 8); (8; 4); (9; 0); (9; 6).
Рассмотрим утверждение ""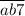 делится на 7"". Если 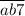делится на 7, то 
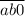делится на 7, 
делится на 7. Из ранее выписанных пар только пары (4; 2); (8; 4) удовлетворяют этому условию.
Мы учили делимость на 3, 4 и 7. Делимость на 2, 5 и 6 будет выполняться автоматически. Проверим делимость на 8. Число 428 не делится на 8, а число 848 делится на 8.
Число 841, очевидно, делится на 1, а число 849 не делится на 9. Значит, это числа от 841 до 848, а сумма цифр наименьшего числа равна 8+4+1=13.
ответ: 13
1)1000:250=4(раза)
2)60*4=240(руб.)
ответ:240 руб. стоит 1кг мармелада из первой упаковки
2)300г за 69 руб.
1)1000:300=1000/300(раза)
2)1000/300*69=230(руб,)
ответ:230 руб. стоит 1кг мармелада из второй упаковки
3)250г за 59 руб.
1)1000:250=4(раза)
2)59*4=236(руб.)
ответ:236 руб. стоит 1 кг мармелада из третьей упаковки
4)325г за 78 руб.
1)1000:325=1000/325
2)1000/325*78=240(руб.)
ответ:240 руб. стоит 1 кг мармелада из четвертой упаковки
ответ: наименьшая цена за 1 кг у мармелада из второй упаковки