В решении.
Пошаговое объяснение:
1) |x| < 7
Схема:
x < 7 x > -7
Решение неравенства: х∈(-7; 7), пересечение.
Входят в решения неравенства: -6; 0; 4.
Неравенство строгое, скобки круглые.
2) |x| <= 11
Схема:
x <= 11 x >= -11
Решение неравенства: х∈[-11; 11], пересечение.
Входят в решения неравенства: -9; -6; 0; 4; 8.
Неравенство нестрогое, скобки квадратные.
3) |x| > 1
Схема:
x > 1 x < -1
Решение неравенства: х∈(-∞; -1)∪(1; +∞), объединение.
Входят в решения неравенства: -20; -9; -6; 4; 8; 15.
Неравенство строгое, скобки круглые.
4) ) |x| >= 5
Схема:
x >= 5 x <= -5
Решение неравенства: х∈(-∞; -5]∪[5; +∞), объединение.
Входят в решения неравенства: -20; -9; -6; 8; 15.
Неравенство нестрогое, скобки квадратные, а знаки бесконечности всегда с круглой скобкой.
4/Задание № 6:
На кухне мальчики сидят на трёхногих табуретках, а девочки на четырёхногих. Всего на кухне 50 ног (считаются ноги детей и табуреток). Сколько в комнате мальчиков, если девочек не менее одной?
Пусть мальчиков m, а девочек d. Тогда:
(3+2)*m+(4+2)*d=50
5m+6d=50
Так как 5m и 50 делится на 5, то и 6d должно делиться на 5. Это выполняется только тогда, когда d делится на 5.
Так как d>0, то проверку начинаем с d=5:
d=5: 5m+6*5=50; 5m+30=50; 5m=20; m=4
d=10: 5m+6*10=50; 5m+60=50; 5m=-10; m=-2 - отрицательное число мальчиков быть не может
ОТВЕТ: 4 мальчика
т.к. f(x) всегда положительна, то наименьшее значение может быть 0 и больше.
Посмотрим, существуют ли а, при которых f(x) принимает значение равное 0 на отрезке [-5;5]. Т.е. задача равносильна задаче
При каких а, у квадратного уравнения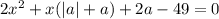 есть корни принадлежащие отрезку [-5;5]
есть корни принадлежащие отрезку [-5;5]
Очевидно, что если 2a-49>0, то решений нет. О.В.Р: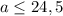
Рассмотрим а=<0. При таких а выражение |a|+a обращается в 0 следовательно вершина лежит на оси х=0
Тогда при а=<0 нам необходимо и достаточно условия f(5)>=0
Почему?
Нарисуем параболлу. Мы видим, что если в точке b(по оси абцисс) параболла принимает положительное значение, то пересечение с осью абцисс лежит левее b
Рассмотрим а>0
Вершина параболлы будет лежать в 3 четверти координатной плоскости(где x и y отрицательны). Вершина по оси ординат лежит ниже 0 следует из того, что а=<24,5, а то, что вершина лежит левее нуля по оси абцисс следует из того, что |a|+a>0
Поэтому и здесь нам достаточно условия, что f(5)>=0
Теперь наша задача свелась к решению неравенства
f(5)>=0, a=<24,5
В итоге ответ: