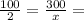
100 и 2 сокращаем. будет 50
а Х преносим.
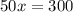
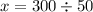
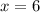
ответ: х=6
можно как лучший ответ
470-(500-25*3)=45
Сначало решаем в скобках. Первое делаем * потом -.
Потом отнимаем от 470 то что потучилось в скобках.
(300+160:4) : 2=170
Сначало решаем в скобках. Первое : потом +.
Потом то что получилось в скобках : на 2.
500+(400-160+40)=780
Сначало решаем в скобках. Первое + потом -.
Потом к 500+ то что получилось в скобках.
(870 - 240 * 3) : 5=30
Сначало решаем в скобках. Первое * потом -
Потом то что полусилось в скобках : на 5.
(120-80):(100:25)=10
Сначало решаем в скобках с : потом с -.
Потом : то что получилось в первых скобках, на то что получилось во- вторых.
100-32*(87-84)=4
Сначало делаем в скобках, потом *, потом -.
280-140*2+7=7
Сначало *, потом -, потом+
81:3*2:3=18
Сначало :, потом *.
У нины было 50 рублей. и еще 8 монет, по пять рублей.каждая. Сколько всего денег было у Нины?
Определяем сколько было денег пярублевыми монетами:
5*8=40
Складываем 50 рублей и 40 рублей пятирублевыми монетами:
50+40=90
ответ: 90 рублей.
В 2 одинаковых спальных вагонах поезда 120 мест. Сколько мест в 7 таких вагонах? в 10 таких вагонах?
Определяем сколько мест в 1 вагоне:
120:2=60
Зная сколько мест в 1 вагоне можно определить сколько мест в 7 и 10 вагонах:
60*7=420
60*10=600
ответ: в 7 вагонах 420 мест
в 10 вагонах 600 мест.
Правила умножения и деления алгебраических дробей
Умножение и деление алгебраических дробей выполняется по тем же правилам, по которым проводятся соответствующие действия с обыкновенными дробями. Напомним их.
Нам известно, что при умножении обыкновенных дробей отдельно перемножаются числители и отдельно – знаменатели, первое произведение записывается числителем, а второе – знаменателем. Например, .
А деление обыкновенных дробей заменяется умножением на дробь, обратную делителю. К примеру, .
Теперь можно увидеть отчетливое сходство с правилами умножения и деления алгебраических дробей, которые мы сейчас и сформулируем.
Умножение двух и вообще любого числа алгебраических дробей в результате дает дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей перемножаемых дробей. Этому правилу отвечает равенство , где a, b, c и d – некоторые многочлены, причем b и d – ненулевые.
Чтобы разделить одну алгебраическую дробь на другую, нужно первую дробь умножить на дробь, обратную второй. То есть, деление алгебраических дробей выполняется следующим образом , где a, b, c и d – некоторые многочлены, причем b, c и d – ненулевые.
Здесь стоит обратить внимание на то, что под алгебраической дробью, обратной данной, понимают такую дробь, произведение которой с исходной тождественно равно единице. То есть, взаимно обратные алгебраические дроби определяются аналогично взаимно обратным числам. И из того, как мы определили умножение алгебраических дробей, следует, что взаимно обратные алгебраические дроби различаются тем, что у них числители и знаменатели переставлены местами. Например, обратной к алгебраической дроби будет дробь .
Пошаговое объяснение:
Відповідь:
х=6
Покрокове пояснення: