д)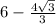 
Пошаговое объяснение:
Известно, что гипотенуза АС прямоугольного треугольника АВС равна 10 и ∠ВАС=60°.
Определим длины катетов АВ и ВС:
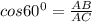
AB=AC·cosn60°=10·1/2=5,
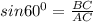
BC=AC·sins60°=10·√3/2=5√3.
Собака с поводком длиной 2 двигаясь по катетам АВ и ВС прямоугольного треугольника АВС может достичь (см. рисунок) все точки от А по N и от L по C.
Поэтому, чтобы определить длина части отрезка АС, то есть длину отрезка NL, до которой собака не может добраться определим длину отрезка АN и LC.
Так как ∠MAN=∠BAC, ∠AMN=∠ABC=90°, ∠ANM=∠ACB, то
треугольники ΔAMN и ΔABC подобны. Тогда из-за подобия треугольников ΔAMN и ΔABC:
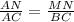или AN=AC·MN/BC=10·2/(5√3)=4/√3=4√3/3.
Также ∠LCK=∠ACB, ∠LKC=∠ABC=90°, ∠CLK=∠CAB, то
треугольники ΔLKC и ΔABC подобны. Тогда из-за подобия треугольников ΔLKC и ΔABC:
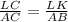или LC=AC·LK/AB=10·2/5=4.
Тогда длина части отрезка АС, до которой собака не может добраться
NL=AC-АN-LC=10-4√3/3-4=6-4√3/3.
1.а) 2/5, что составляет 2/5*100-=40% ; б)75/50=3/2, что составляет 3/2*100=150%; в) 7/20, что составляет 7/20=35%; г)40/32=1,25, что составляет 1,25*100=125%.
2. Осталось 620-200=420 г сыра, что составляет 420/600=21/30 часть всего сыра.
3, а).Лисичек будет 123-45=78, что составляет 78/123=26/41 часть от всех грибов.
3. Обозначим искомое число через x.Тогда 2/3 от х равно 2/3*х (две третих, умноженное на х).Обозначим эту часть через у, то есть у=2/3*х. Но по условию 1/3 от у равна 6, то есть 1/3*у=6.Подставим вместо у выражение: 1/3*2/3*х=6. Отсюда 2/9*х=6, х=9/2*6=27.