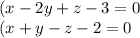
ответ:
вторая мировая война[24] (1 сентября 1939 — 2 сентября 1945[25]) — война двух мировых военно-политических коалиций, ставшая крупнейшим вооружённым конфликтом в человечества.
вторая мировая война
ww2montage.png
по часовой стрелке, начиная с левого верхнего угла: первое сражение при эль-аламейне; китайцы, заживо погребённые японскими солдатами; советские войска во время зимнего наступления; японские самолёты готовятся взлететь с авианосца сёкаку; знамя победы над рейхстагом; подводная лодка во время атаки
ответ:
любой член прогрессии может быть вычислен по формуле
{\displaystyle b_{n}=b_{1}q^{n-1}.} {\displaystyle b_{n}=b_{1}q^{n-1}.}
если {\displaystyle b_{1}> 0} {\displaystyle b_{1}> 0} и {\displaystyle q> 1} {\displaystyle q> 1}, прогрессия является возрастающей последовательностью, если {\displaystyle 0
своё название прогрессия получила по своему характеристическому свойству:
{\displaystyle |b_{n}|={\sqrt {b_{n-1}b_{n+1}}},} {\displaystyle |b_{n}|={\sqrt {b_{n-1}b_{n+1}}},}
то есть модуль каждого члена равен среднему его соседей.
пошаговое объяснение:
Направляющий вектор прямой, образованной пересечением двух плоскостей А1x+B1y+C1z+D1=0 и A 2 x+B2y+C2z+D2=0, будет перпендикулярен нормальным векторам
→n1=(A1, B1, C1) и →n2=(A2, B2, C2 )
. То есть в качестве направляющего вектора мы может взять произведение векторов
→ n1=(A1, B1, C1) и →n2=(A2, B2, C2).
Нормальные векторы исходных плоскостей n1(1,-2,1) и n2(1,1,-1).
Находим их векторное произведение.
i j k| i j
1 -2 1| 1 -2
1 1 -1| 1 1 = 2i + 1j + 1k + 1j - 1i + 2k = 1i + 2j + 3k.
Нашли направляющий вектор прямой, по которой пересекаются исходные плоскости: n(1; 2; 3).
Этот вектор является нормальным вектором перпендикулярной плоскости.
Её уравнение: 1(x - 1) + 2(y + 2) + 3(z - 1) = 0.Раскроем скобки.
x - 1 + 2y + 4 + 3z - 3 = 0 или x + 2y + 3z = 0.
ответ: x + 2y + 3z = 0.