Саму задачу можно переформулировать немного по-другому:
Было: Расставить минимальное количество шашек на шахматной доске 8 на 8, так чтобы было невозможно поставить коня так, чтобы он не бил ни одной шашки.Переходит в: расставить на доске минимальное количество коней так, чтобы было невозможно поставить шашку не под удар коня.Если мы решим вторую задачу, то просто нужно будет заменить коней шашками - и мы получим искомое расположение.
По поводу второй задачи можно заметить, что:
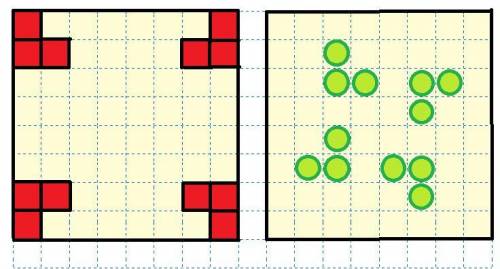
Разные кони должны бить выделенные красным клетки на рисунке ниже.Отсюда следует, что мы не можем расставить менее, чем 4 * 3 = 12 коней. Если это можно сделать, то задача решится. И да, это получилось сделать (рисунок 2).
Заменяем коней шашками и получаем ответ: 12 коней.
ответ: 12 шашек.
ответ: нет . Более того , невозможно получить произвольное натуральное число N.
Пошаговое объяснение:
Найдем среди чисел от 2 жо 1994 число содерщащее в делителях максимальную степень двойки.
Такое число единственно и равно : 2^10=1024
Предположим , что произвольная комбинация + ,- из слагаемых :
1/2 ;1/3 ; 1/4 1/994 равна натуральному числу N.
Тогда умножим обе части равенства на 2^10.
Во всех дробях вида : 2^10/k сократяться со знаменателем все степени числа 2, что содержит число k. (То есть знаменатели всех дробей станут нечетными) . Если число k отлично от 2^10 , то числители этих дробей будут четны , тк все эти числа содержат в себе меньше чем 2^10.
Но если число k=2^10=1024 , то это единственное число которое после сокращения имеет нечетный числитель равный 1. Другими словами это будет просто число 1 (2^10/2^10)=1.
Всего от 2 до 1994 : 1993 числа , одно из которых равно единице , а остальные имеют четные числители и нечетные знаменатели.
Если перенести единицу в правую часть равенства , то получим cправа:
2^10*N +-1 - абсолютно очевидно , что число справа является нечетным. (+- в зависимости от того какой знак стоит перед ним)
А слева у нас остается 1992 числа с четными числителями и нечетными знаменателями. Если привести каждую из данных дробей к общему нечетному знаменателю ( тк общий знаменатель нечетных чисел число нечетное) , то получим дробь с нечетным знаменателем и числителем состоящим сумм и разностей четных чисел. ( Cумма или разность в любых комбинациях произвольного числа четных чисел число четное)
Таким образом получаем :
A/B= 2^10 *N+-1=C
A-четное число
B-нечетное число
2^10*N +-1=C -нечетное число
Но тогда :
A=B*C -то есть мы получили, что произведение двух нечетных чисел равна четному числу. Мы пришли к противоречию.
Нельзя расставить знаки «+». «-» между дробями 1/2,1/3,1/4...1/1994 так , чтобы в результате получилось натуральное число. Cоответственно число 4 не является исключением из правил и его так же получить невозможно.