Пусть объём бассейна равен 1, тогда время его заполнения до ремонта первым насосом – x, а вторым – y часов. Следовательно, 1/x - производительность первого насоса до ремонта, а 1/y - производительность второго насоса до ремонта. Зная, что бассейн до ремонта насосов заполняется за 8 часов, то составим первое уравнение: 8(1/x+1/y)=1, т.е. 8/x+8/y=1.
1,2(1/x) - производительность первого насоса до ремонта, а 1,6(1/y) - производительность второго насоса после ремонта. Зная, что бассейн после ремонта насосов заполняется за 6 часов, то составим второе уравнение: 6(12/x+16/y)=1, т.е. 7,2/x+9,6/y=1.
Решив совместно эти два уравнения , получаем : x=12, y=24.
Из найденных значений для x и y вычислим производительность первого насоса после ремонта: 1,2(1/x)=(1,2*1)/12=0,1
По формуле t=A/P найдём время наполнения бассейна при работе только первого насоса после ремонта: 1/0,1=10 ч.
ответ: 10 ч.
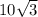, а угол при основании 30, и зная, что катет напротив угла в 30 градусов = половине гипотенузы, то этот катет, она же высота =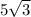 
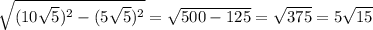
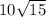
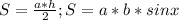
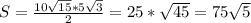
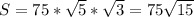
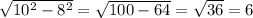
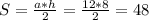
1:9= 0,1111111 ; 1:6=0,16666666
1 1/9 = 1 ,111
2 1/9 = 2, 111
-3 1/9= -3, 111
-1/9 = -0,111
1/6= 0,166
4 1/6 = 4,166
-5 1/6 = -5 ,166
-7 1/6 = -7, 166