ответ:Биссектриса делит угол, из которого выходит, пополам. От сюда, можно узнать что углы ∠ABD и ∠DBC=80/2=40°
Рассмотрим треугольник ABD, в нем мы знаем два угла: ADB и ABD. Зная два угла в треугольнике можно найти третий угол, т. к. сумма углов в треугольнике равна 180°. Тогда: 180°-(40°+120°)=20°. Т. е. угол ∠DAB = 20°;
Теперь рассмотрим треугольник ABC, в нем мы теперь знаем два угла: ∠A (равен углу ∠DAB ) и угол ∠B, отсюда можно найти третий угол ∠C: 180°-(20°+80°)=80°.
Рассмотри треугольник DBC, в нем нам известны два угла ∠DBC и ∠C, найдем третий угол: 180°-(40°+80°)=60°.
ответ: В треугольнике CBD углы: ∠CBD=40°, ∠C=80°, ∠CDB=60°.
Заметим для начала, что операция коммутативна
Проверим, может ли при каких-то a и b из G получиться в результате операции число не из G (то есть -1, так как, очевидно, результат операции - действительное число)
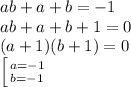
То есть посредством операции нельзя выйти из R\{-1}
Найдем нейтральный элемент по этой операции:
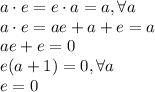- нейтральный элемент существует
Проверим свойство ассоциативности:
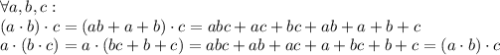- выполнено
Посмотрим, у каждого ли есть обратный элемент. Рассмотрим произвольный элемент a:
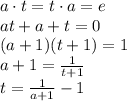
Обратный существует (так как a не равен -1), а также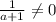 
, то есть значение выражения для t не может быть -1, а отсюда t лежит в G.
Таким образом, G - абелева группа.
1) пусть вершины квадрата, лежащие на оси абсцисс имеют координаты (-а; 0) и (а; 0) (т.е симметричны относительно оси координат, иначе одна из вершин не попадёт на параболу)
2) тогда ординаты точек пересечения второй пары вершин квадрата с параболой будут: (-а)² и (а)² или у=а²(высота квадрата)
3) имеем по построению ширину(т.е расстояние между вершинами квадрата на оси абсцисс) квадрата а+[-a]=2a
4) Площадь квадрата: 2а×а²=2а³
Замечание: в условии задания сказано о квадрате, а у квадрата все стороны равны. Но по логике наших рассуждений получили стороны 2а ≠ а². Значит это прямоугольник, а не квадрат.
Пошаговое объяснение: