S= ah/2
Это прямоугольный треугольник.
Один из катетов всегда совпадает с высотой.
Площадь прямоугольного треугольника равна половине произведения катетов.
S пр.тр. = а•в/2, где а и в - катеты.
Известен только один катет 32.
Можно найти другой катет по теореме « Сумма квадратов катетов равна квадрату гипотенузы»:
а^2 + в^2 = с^2, где а и в - катеты, с - гипотенуза.
Значит,
в^2 = с^2 - а^2
в^2 = 40^2 - 32^2
в^2 = 1600 - 1024 = 576
в = 24 - второй катет.
S пр.тр. = а•а
S пр.тр. =32•24 = 768 квадратных единиц- площадь прямоугольного треугольника.
ответ: 768.
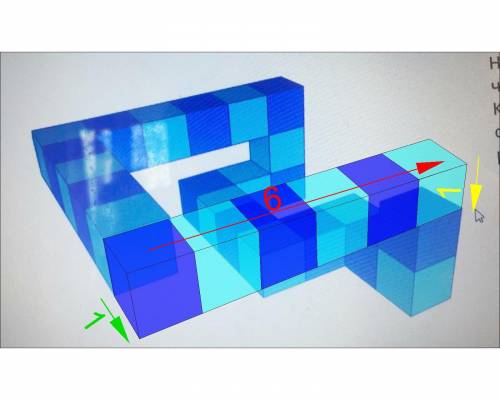
6
Пошаговое объяснение:
Для правильного решения задания нужно внимательно рассмотреть рисунок и поочерёдно просчитать смещение относительно начального кубика в трёх направлениях.
На первом рисунке показаны смещение вдоль оси z - жёлтым цветом, вдоль оси у - зелёным цветом, вдоль оси х - красным цветом.
Посчитаем, как сместилась конечная точка от начальной:
х: -3+3-6 = -6
у: 2+4-5 = 1
z: -2+3 = 1.
Значит нужно из конечной точки сместиться на:
-1 вдоль оси у,
+6 вдоль оси х,
-1 вдоль оси z.
На втором рисунке мы видим что смещение на -1 вдоль оси у и -1 вдоль оси z обеспечивается стыковкой горизонтальной полосы из 6 кубиков, которые дают смещение на +6 вдоль оси х.

Пошаговое объяснение:
х - задуманное число
х+1 1\6х+9 1\6х=43 1\3
11 2\6х=43 1\3
11 1\3х=43 1\3
х=43 1\3:11 1\3
х=130\3*3\34
х=130\34=3 14\17 - задуманное число