Основная логика решения заключаеться в том, что нам нужно упростить выражение, иначе мы его не посчитаем. Для этого можно присмотреться к степеням, и увидеть что они кратны 7 . Тогда получаеться:
1)
Так как у нас есть общая степень 7, то мы можем ее не учитывать при сравнении. Из этого следует, что нам нужно сравнивать:
2)
Если на этом этапе вы можете точно определить, какое число больше, значит задача решена, но для тех кто не уверен, можно пойти дальше. Выражения с обеих сторон можно представить в виде произведений с одинаковыми степенями:
3)
Теперь видно, что у нас есть пара степенных выражений с общим основанием, и мы можем их легко сравнить:
4)
Теперь мы знаем, что первая часть левого выражения больше первой правого. Дальше нам нужно сравнить вторые части обоих выражений, а тут уже нужно вспомнить таблицу умножения:
5)
Мы видим, что первое сравнение и второе не совпадают по знаку, тогда берем большее выражение из обоих неравенств и сравниваем между собой:
ответ: угол А=80 градусов, угол В= 90 градусов, угол С= 100 градусов, угол Д=90 градусов Принцип решения: 1) пусть точка О - центр окружности с диаметром АС, значит диагональ АС четырехугольника проходит через центр окружности О 2 ) треугольник ВОС - равнобедренный ВО=СО (т. к. точки В и С лежат на окружности) , значит угол ОВС= углу ОСВ. Угол ВОС=100 градусам (т. к. дуга ВС=100 градусов) , значи углы ОВС и ОСВ по 40 градусов каждый (т. к. сумма трех углов в треугольнике = 180 градусам) 3) Аналогичные рассуждения для треугольника СОД, который тоже равнобедренный: угол СОД=60 градусов (т. к. дуга СД=60 градусов) , тогда угол ОДС = углу ОСД = 60 градусов 4) Для треугольника АОВ: угол АОВ= угол АОС-угол ВОС=180-100=80 градусов. Аналогичные рассуждения для треугольника АОВ, который тоже равнобедренный, тогда угол ОАВ = углу ОВА = 50 градусов 5) Для треугольника АОД угол АОД= угол АОС-угол СОД=180-60=120 градусов. Аналогичные рассуждения для треугольника АОД, который тоже равнобедренный, тогда угол ОАД = углу ОДА = 30 градусов 6) в четырехугольнике угол А (угол ДАС) =угол ОАД+угол ОАВ=30+50=80 градусов 7) в четырехугольнике угол В (угол АВС) =угол ОВА+угол ОВС=50+40=90 градусов 8) в четырехугольнике угол С (угол ВСД) =угол ОСВ+угол ОСД=40+60=100 градусов 9) в четырехуголинике угол Д (угол СДА) =угол ОДС+угол ОДА=60+30=90 градусов
Пошаговое объяснение:
Основная логика решения заключаеться в том, что нам нужно упростить выражение, иначе мы его не посчитаем. Для этого можно присмотреться к степеням, и увидеть что они кратны 7 . Тогда получаеться:
1)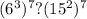
Так как у нас есть общая степень 7, то мы можем ее не учитывать при сравнении. Из этого следует, что нам нужно сравнивать:
2)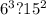
Если на этом этапе вы можете точно определить, какое число больше, значит задача решена, но для тех кто не уверен, можно пойти дальше. Выражения с обеих сторон можно представить в виде произведений с одинаковыми степенями:
3)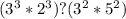
Теперь видно, что у нас есть пара степенных выражений с общим основанием, и мы можем их легко сравнить:
4)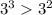
Теперь мы знаем, что первая часть левого выражения больше первой правого. Дальше нам нужно сравнить вторые части обоих выражений, а тут уже нужно вспомнить таблицу умножения:
5)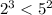
Мы видим, что первое сравнение и второе не совпадают по знаку, тогда берем большее выражение из обоих неравенств и сравниваем между собой:
6)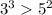
Из этого следует что: