Пошаговое объяснение:
Скорее всего 1
Пошаговое объяснение:
Чтобы решить данную задачу - нужно помнить теорию о тригонометрических функция:
Рассмотрим треугольник АВС:
1. Он равнобедренный
2. Разделён на два прямоугольных треугольника
3. Проведена медиана AK
a) Теперь найдём синус угла А или sin ∠A:
Рассмотрим ΔABH:
AB=10 и AH=1/2*AC=6
sin ∠A находится через отношения :
sin ∠A = BH/AB
Найдём BH через теорему Пифагора:
BH = 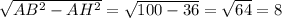
И вычислим синус :
sin ∠A = 8/10 =0,8
b) Косинус находится через отношение п:
cos ∠C = HC/BC
Подставим значения:
cos ∠C = 10/6=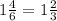
в) Тангенс угла CBH находится отношением:
tg ∠CBH = BH/HC
Подставим значения:
tg ∠CBH = 8/6=4/3=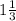
г) Найдём сначала синус угла ABC
Найдём синусы углов ABH и HBC:
sin ABH =AH/AB ; sin HBC = HC/BC
sin ABH = 0,6 ; sin HBC = 0,6
sin ABC = sin ABH + sin HBC =1,2
Заметим sin ABC=sin ABK =1,2 ,поэтому найдём высоту AK:
sin HBC = AK/AB => AK=sin HBC * AB => AK=1,2*10=12
нод
а) 4 б) 25
нок а) 60 б) 150
Пошаговое объяснение:
б)
Наибольший общий делитель (НОД) двух данных чисел 50 и 75 — это наибольшее число, на которое оба числа 50 и 75 делятся без остатка.
НОД (50; 75) = 25.
Как найти наибольший общий делитель для 50 и 75
Разложим на простые множители 50
50 = 2 • 5 • 5
Разложим на простые множители 75
75 = 3 • 5 • 5
Выберем одинаковые простые множители в обоих числах.
5 , 5
Находим произведение одинаковых простых множителей и записываем ответ
НОД (50; 75) = 5 • 5 = 25
НОК (Наименьшее общее кратное) 50 и 75
Наименьшим общим кратным (НОК) 50 и 75 называется наименьшее натуральное число, которое само делится нацело на каждое из этих чисел (50 и 75).
НОК (50, 75) = 150
Как найти наименьшее общее кратное для 50 и 75
Разложим на простые множители 50
50 = 2 • 5 • 5
Разложим на простые множители 75
75 = 3 • 5 • 5
Выберем в разложении меньшего числа (50) множители, которые не вошли в разложение
2
Добавим эти множители в разложение бóльшего числа
3 , 5 , 5 , 2
Полученное произведение запишем в ответ.
НОК (50, 75) = 3 • 5 • 5 • 2 = 150
а)
Наибольший общий делитель (НОД) двух данных чисел 12 и 20 — это наибольшее число, на которое оба числа 12 и 20 делятся без остатка.
НОД (12; 20) = 4.
Как найти наибольший общий делитель для 12 и 20
Разложим на простые множители 12
12 = 2 • 2 • 3
Разложим на простые множители 20
20 = 2 • 2 • 5
Выберем одинаковые простые множители в обоих числах.
2 , 2
Находим произведение одинаковых простых множителей и записываем ответ
НОД (12; 20) = 2 • 2 = 4
НОК (Наименьшее общее кратное) 12 и 20
Наименьшим общим кратным (НОК) 12 и 20 называется наименьшее натуральное число, которое само делится нацело на каждое из этих чисел (12 и 20).
НОК (12, 20) = 60
Как найти наименьшее общее кратное для 12 и 20
Разложим на простые множители 12
12 = 2 • 2 • 3
Разложим на простые множители 20
20 = 2 • 2 • 5
Выберем в разложении меньшего числа (12) множители, которые не вошли в разложение
3
Добавим эти множители в разложение бóльшего числа
2 , 2 , 5 , 3
Полученное произведение запишем в ответ.
НОК (12, 20) = 2 • 2 • 5 • 3 = 60
444444444⁴44444444444