1) По формуле сложения сворачиваем, получается:
cos (128+52)=cos 180= -1
2) Я, так понимаю, косинус найти нужно?
Если так, то:
применяем основную тригонометрическую формулу sin^2 x+cos^2 x =1, подставляем все известные и решаем:
cos^2 x=1-(144/169)
cos^2 x=25/169
cosx = 5/13, но поскольку косинус во 2 четверти отрицательный, то ответ -5/13
3)2sin+sqrt2 = 0 (sqrt - корень)
2sin = -sqrt2
sin = -sqrt2/2
x=(-1)^k+1 * 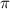 /4+2
/4+2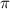 n, n
n, n  z
z
4) tg^2 x - tgx = 0
Выносим tgx за скобку:
tgx(tgx-1)=0
tgx=0 tgx-1=0
x = 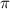 n, n
n, n  z tgx=1
z tgx=1
x=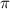 /4+
/4+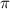 n, n
n, n  z
z
Для чего используют отрицательные числа, ведь вместо них можно запросто использовать системы с точкой отсчета от нуля и выше.
Например темепературная шкала кельвина, там нет отрицательных велечин, есть только абсолютный нуль. На мой взгляд отрицательные числа - это исключительно абстрактная велечина, в природе не существует ничего отрицательноего (даже заряженные частицы названы так для удобства). Наиболее "правильные" на мой взгляд являются понятие "дебета" и "кредита". У меня, например в кармане не может лежать минус 100 рублей, минимальное значение - это 0. Но мой долг может быть равен 100.
а=5,9 см
б=4 см
с=12 см
V=a*б*с=5,9*4*12=283,2 кум.см
S=2*(аб+бс+са)=2*(5,9*4+4*12+12*5,9)=2*(23,6+48+70,8)=2*142,4=284,8 кв.см
L=4*(а+б+с)=4*(5,9+4+12)=4*21,9=87,6 см