У подобных фигур соответственные стороны имеют одинаковое отношение. У прямоугольников все углы прямые и противоположные стороны равны, то есть определять их подобие достаточно по двум смежным сторонам.
1)
AB:KL = 32см÷16см = 2
BC:LM = 24см÷12см = 2
2=2, значит прямоугольник ABCD подобен KLMN с коэффициентом 2.
3)
BC = KL = 7мм -- прямоугольники могут иметь коэф. подобия 1 (быть равными), НО AB = 5мм ≠ LM = 10,8мм.
Прямоуг. могут быть подобны по другим сторонам.
KL:AB = 7мм÷5мм = 1,4
LM:BC = 10,8мм÷7мм = 54/35
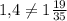
Если KLMN не подобен ABCD, то ABCD не подобен KLMN.
Прямоугольник ABCD не подобен KLMN.
14-12,725=1,275
1,275*12,4=15,81
11,2-7,95=3,25
2,6:3,25=0,8
15,81-0,8=15,01
2) 3/4 : 5/6 + 2 1/2 * 2/5 - 1 : 1 1/6 =1 3/70
3/4:5/6=3/4*6/5=9/10
2 1/2*2/5=5/2*2/5=1
1:1 1/6=1*6/7=6/7
9/10+1=1 9/10
1 9/10-6/7=1 63/70-60/70=1 3/70
3) ( 2/15 + 7/12) * 30/43 - 2 : 2 1/2 * 5/32=3/8
2/15+7/12=8/60+35/60=43/60
43/60*30/43=1/2
2:2 1/2=2*2/5=4/5
4/5*5/32=1/8
1/2-1/8=4/8-1/8=3/8
4) (7 - 8 4/5) * 2 7/9 - 15 : (1/8 - 3-4) =-2 9/11
7 8 4/5=-1 4/5
-1 4/5*2 7/9=-9/5*25/9=-5
1/8-7 =-6 7/8
15:(-6 7/8)=-15*8/55=-24/11=-2 2/11
-5-(-2 2/11)=-5+2 2/11=-2 9/11