Пошаговое объяснение:
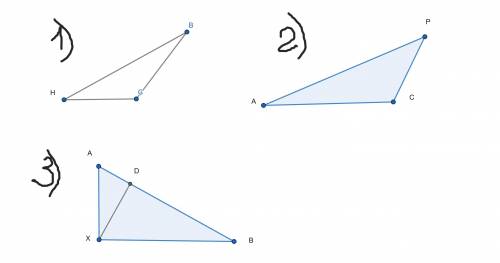
1) НВ-наибольшая сторона, а значит напротив нее лежит наибольший угол. ∠С=124°. 180°-(124°+40°)=16°- третий угол треугольника НВС.
∠В=16° , так как он лежит напротив наименьшей стороны треугольника.
∠Р=40°
2) Пусть ∠Р=х°, тогда ∠С=12х°. ∠А=50° по условию, а так как сумма углов в любом треугольнике = 180°. Составим уравнение:
х+12х+50°=180°
13х=180°-50°
13х=130°
х=130°:13
х=10°
Значит ∠Р=10°, ∠С=10°*12=120°
ответ: 10°, 120°,
3) Наверное в условии не СD, а ХD - высота.
ΔАВХ-прямоугольный, значит ∠А+∠В=90°, значит ∠А=90°-∠В=90°-35°=55°
ΔАХD-прямоугольный, а значит ∠А+∠АХD=90°
∠АХD=90°-∠А=90°-55°=35°
ответ : 35°
В классе всего 12 + 18 = 30.
1) Вероятность выбрать первого мальчика равна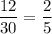
. Одного человека мы выбрали уже, тогда в классе остается 11 мальчиков и 18 девочек. Вероятность выбрать второго мальчика равна 
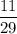. По теореме умножения, искомая вероятность: 
2) Выбрать первую девочку можно с вероятностью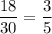
. В классе остается 29 человек из них 17 девочек. Вероятность выбрать вторую девочку равна 
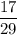. По теореме умножения, искомая вероятность: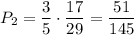 
3) Вероятность того, что среди двух выбранных человек окажутся девочка и мальчик, равна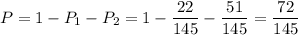
ответ: 1) 22/145; 2) 51/145; 3) 72/145.