а) данная модель распределена по биномиальному закону.Вероятность успеха в одном испытании равна p = 100/10000 = 0.01, тогда q = 1 - p = 1 - 0.01 = 0.99
б) Вероятность того, что среди купленных фирмой билетов окажется не более четырех выигрышных, равна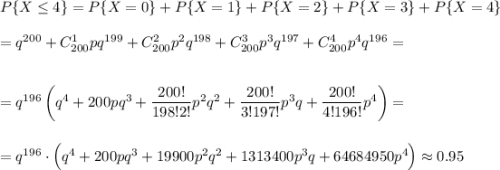
в) Воспользуемся вероятностью противоположного события.
Подсчитаем сколько нужно взять билетов, чтобы среди них с вероятность 100% - 90% = 10% оказались все не выигрышные билеты.
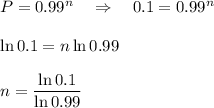
Откуда n = 230, так как вероятность того, что купленные билеты невыигрышные равна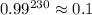 
откуда вероятность того, что среди купленных билетов окажутся хотя бы один выигрышный билет равна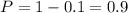 
Пошаговое объяснение:
1. а). Вероятность первый свежий 9/21=3/7, второй свежий 8/20=2/5.
Вероятность двух свежих 3/7*2/5=6/35≈0,17
б). Вероятность первый свежий 9/21=3/7, второй солёный 12/20. Вероятность этого события 3/7*12/20=36/140=9/35
Вероятность первый соленый 12/21, второй свежий 9/20. Вероятность этого события 12/21*9/20=108/420*9/35
Вероятность искомого 9/35+9/35=18/35≈0,51
2. Вероятность белого 3/5=0,6
3. Вероятность первого черного 5/10, вероятность второго черного 4/10, вероятность 3 черного 3/10. Вероятность, что 3 шара черные 5/10*4/10*3/10=6/100=0,06