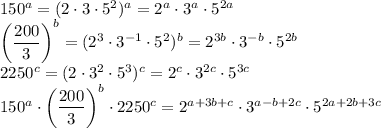
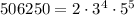, то равенство при целых a, b, c будет в том и только в том случае, если будет выполняться система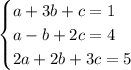
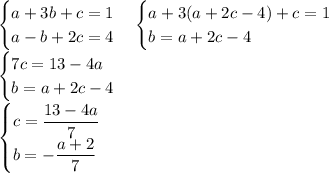
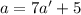. Подставляем: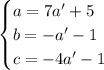
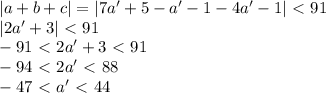
1
В принципе, тут всё устно находится: перебираем случаи z=9,8,...,1,0, и имеем сумму (5+6+...+10)+9+8+7+6=75.
Но можно посчитать и для более общего случая (такая задача возникает при подсчёте числа счастливых билетов). Уравнение x+y+z=k имеет f(k)=(k+2)(k+1)/2 решений в целых неотрицательных числах, что можно найти или через число сочетаний с повторениями из 3 по k, или как сумму чисел от 1 до k+1 для x=k,k-1,...,1,0. Если k<=9, то решений в десятичных цифрах столько же. При k>=10 появляются "лишние" решения, то есть такие, где x>=10 или y>=10 или z>=10. Если x>=10, то полагаем x'=x-10 и находим число решений для уравнения x'+y+z=k-10, которое находится по той же формуле, что и выше, с заменой k на k-10. Столько же "лишних" решений для случаев y>=10 и z>=10. При k<=19 неравенства не могут выполняться одновременно. Это даёт ответ f(k)-3f(k-10). При k=13 имеем f(13)-3f(3)=105-30=75
Мы берем две пары (a; b) и (b; c) и составляем новую пару (a; c). Если все такие пары (a; c) также принадлежат множеству, то это множество транзитивно.
Смотрим первое множество.
Берем пару (1; 1). Вторая пара должна начинаться с 1 - возможны два случая: если это пара (1; 1), то новая пара, которую мы составим, - это пара (1; 1), и она также принадлежит множеству. Если вторая пара (1; 3), то новая пара - пара (1; 3) - также принадлежит множеству.
Берем пару (1; 3). Вторая пара должна начинаться с 3 - такая пара только одна (3; 3). На основе этих двух пар составляем новую - (3; 3). Эта пара также принадлежит множеству.
Берем пару (3; 3). Вторая пара должна начинаться с 3 - такая пара только одна (3; 3). На основе этих двух пар составляем новую - (3; 3). Эта пара также принадлежит множеству.
Условие транзитивности выполняется, значит это множество транзитивно.
Смотрим второе множество.
Берем пару (0; 1). Вторая пара должна начинаться с 1 - такая пара только одна (1; 3). На основе этих двух пар составляем новую - (0; 3). Эта пара также принадлежит множеству.
Если рассмотреть оставшиеся пары (0; 3) и (1; 3), то второй пары для них, то есть пары начинающейся с 3, не окажется. Такое тоже допустимо, и это никак не влияет на транзитивность.
Условие транзитивности выполняется, значит это множество транзитивно.