Пошаговое объяснение:
Сначала посчитаем площадь участка ельника. Воспользуемся формулой Пика (рис. 8). Количество внутренних узлов В = 19, количество внешних
узлов Г = 8, тогда площадь фигуры равна = 19 +
8
2
-1 = 22 см2
Учитывая масштаб: 1 см2 = 2002м
2 = 40000 м. S = 22 · 40000 = 880000 м2
.
Т.к. 1 га = 10000 м
2
, следовательно, S = 88 га. В год 88 гектаров еловых насаждений могут удерживать до 88 · 32 = 2816 т. пыли, следовательно за 5 лет – до
14080 т.
Таким образом, формула Пика является универсальной формулой для вычисления площадей (если вершины многоугольника находятся в узлах решетки),
т.е ее можно использовать для любой фигуры. Однако, если многоугольник занимает достаточно большую площадь (или клетки мелкие), то велика вероятность допустить ошибку в подсчетах узлов решетки.
№ 4. x ≤ 0.75
№ 5. ( - ∞; - 1 ] ∪ [ 3; + ∞ )
Пошаговое объяснение:
№ 4. 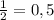
Тогда выражение имеет вид:
(0,5)^ (2*x) ≥ (0.125) ^ (1/2)
(0.5) ^ (2*x) ≥ ((0.5)^3)^(1/2)
(0.5) ^ (2*x) ≥ (0.5) ^ (3*(1/2)
(0.5) ^ (2*x) ≥ (0.5) ^ (3/2)
(0.5) ^ (2*x) ≥ (0.5) ^ 1.5
Т.к. 0,5 < 1, то имеем:
2 * х ≤ 1.5
x ≤ 1.5 / 2
x ≤ 0.75 или иначе записать можно так х ≤ 
№ 5. 7 ^ (x ^ 2) * 49 ^ ( - x) ≥ 343
7 ^ (x ^ 2) * 7^2^ ( - x) ≥ 7 ^ 3
7 ^ (x ^ 2) * 7^ ( - 2 * x) ≥ 7 ^ 3
7 ^ ((x ^ 2) + ( - 2 * x)) ≥ 7 ^ 3
7 ^ (x ^ 2 - 2 * x) ≥ 7 ^ 3
Т.к. 7 > 1, то запишем так:
x ^ 2 - 2 * x ≥ 3
Решим получившееся квадратное неравенство.
x ^ 2 - 2 * x = 3
x ^ 2 - 2 * x - 3 = 0
D = 16
x1,2 = (2±4)/2
x1 = 3 и x2 = -1
Решим методом интервалов.
( - ∞; - 1 ] ∪ [ 3; + ∞ )
43980 тг
Решение на фото.